The Generators of the Automorphism Group of
The following are animations of the generators of the automorphism group of the generalized Petersen
graph , also known as the Möbius-Kantor graph.
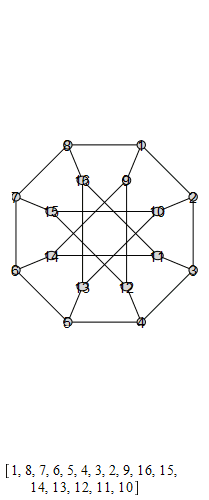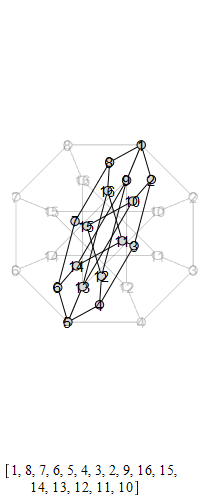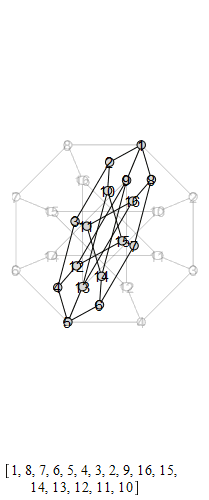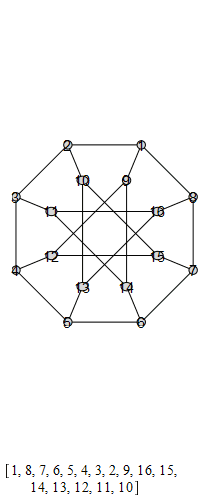
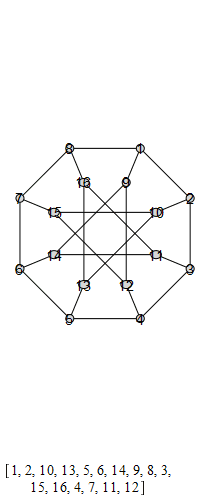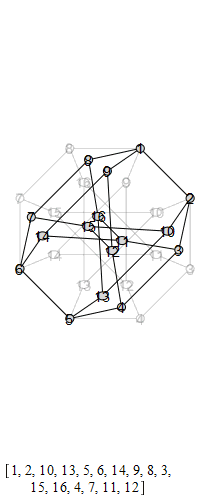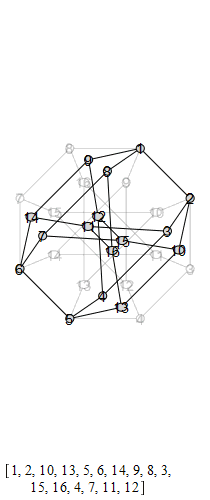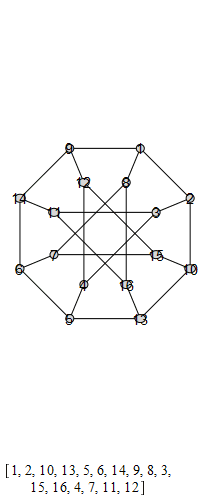
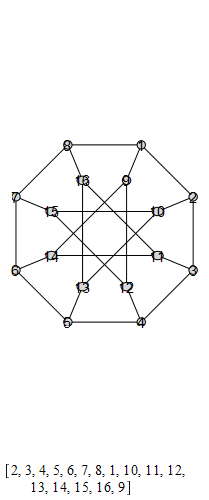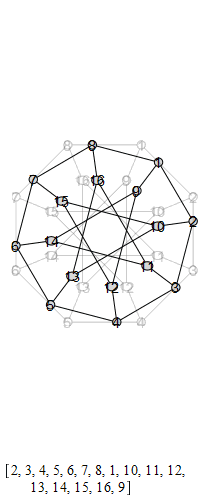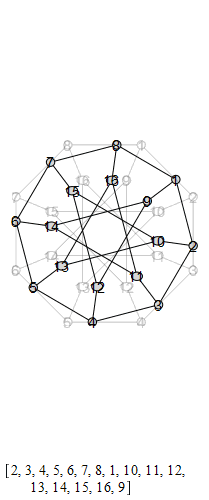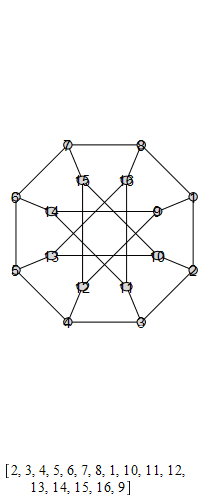
The group that is generated by these is the Tucker Group, and its Cayley graph is super super
cool: it's the only Cayley graph of genus 2. It has 96 elements.
The animations were created using Maple software.


