Things About NAP Scores
I've been thinking a lot about asymmetric graphs this summer. After making my game NAP, I've been thinking
about the best way to make asymmetric graphs. The game works like this: You're given some symmetric graph
and
you need to add vertices and edges economically in order to make the graph asymmetric (i.e. make the graph
have no
nontrivial automorphisms). I
say economically because the goal is to minimize your score, where a new edge
gives you 1 point and a new vertex gives you 2 points. It's a fun daily puzzle and good exercise for those
geometric brain cells. But naturally, I can get a bit competitive with it. It's already tricky sometimes to
get a
reasonably low score for many of the puzzles, but I want the best score.
Since each starting graph is different, there's no way to easily define the best score arbitrarily. Instead, we might ask a better question:
In other words, we want a function W(n) such that if we start with a graph that has n vertices and we score greater than W(n), we are certain we can do better.
Before we start, it'll be helpful to find the smallest asymmetric graph. To do so, we'll start with the following theorem.
Proof.
If \(G\) is symmetric, then there exists some nontrivial automorphism \(A\) of \(G\). We want to show
that \(A\) is
also an automorphism of \(G'\). Let \(V\) be the set of vertices of \(G\). We have for all vertices
\(v\) of \(V\), there is
some vertex \(w\) such that \(A(v) = w\). If \(N_x\) is the set of neighbors of a vertex \(x\) (the set
of all vertices
connected via one edge to x), then, by definition, \(A(N_x) = N_x\). Now let \(v'\) be the corresponding
vertex to \(v\) of \(G'\).
Then, because \(G'\) is the compliment graph of \(G\), \(N_{v'} = V - N_v\). So we have that
\begin{align} A(N_{v'}) &= A(V - N_{v})\\
&= A(V) - A(N_v) \\
&= V - N_v\\
&= N_{v'}.\end{align}
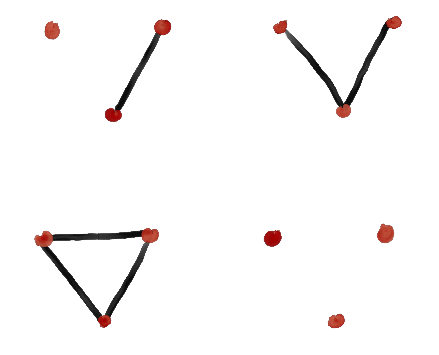
Thus \(A\) is an automorphism of \(G'\). \(\Box\)
Now we can start looking at graphs with a small number of vertices n. When n = 1 or n =
2, it's easy to see there are no asymmetric graphs (ignoring, for convenience, that the graph of 1
vertex is technically asymmetric; we'll see why it's nice to call this symmetric later). When n = 3,
there are only four graphs we
need to check:
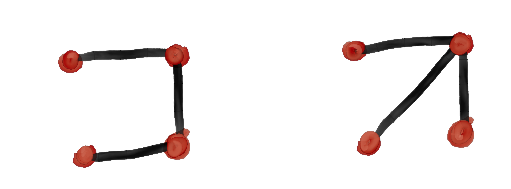
Similarly for graphs of five vertices, we can look at those graphs which are connected and have \(\frac{1}{2}\cdot\begin{pmatrix}5\\2\end{pmatrix} = 5\) edges or less. This ends giving us eight different graphs, which are all also symmetric.
Finally, for graphs of six vertices, we can use the same techniques to find four graphs that are connected
and have \(\lfloor\frac{1}{2}\cdot\begin{pmatrix}6\\2\end{pmatrix}\rfloor = 7\) edges that have no
automorphisms. So, with their compliments, we reach
the eight asymmetric graphs with six vertices:
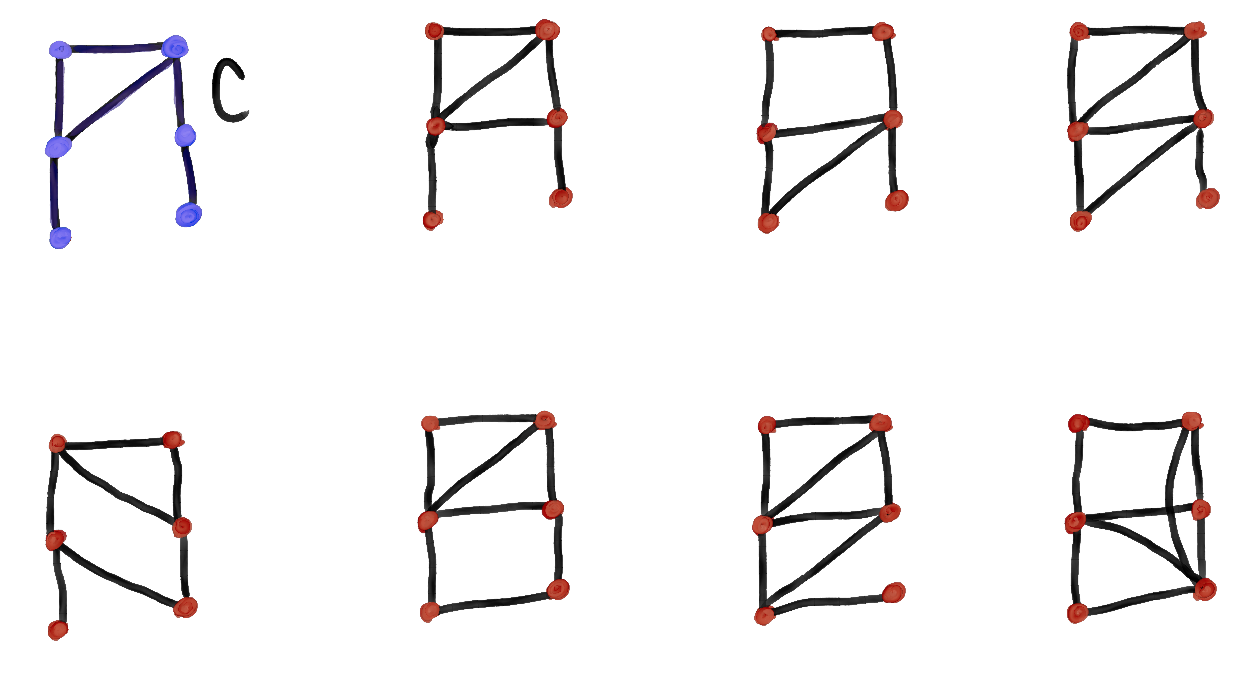
We can see that the graph in blue is the cheapest asymmetric graph, as in it has the fewest nodes and edges. So, when we are solving for W(n) for n < 6, we might consider working towards this cheapest asymmetric graph. Because of this, we will call this graph the cheap ass. graph (for cheap asymmetric graph), or C for short.
To start, when n = 1, we only have one choice for the graph. We need five vertices and 6 edges to get to C, so both the best and worst score for starting with a graph of one vertex is W(1) = 5*2 + 6 = 16. For n = 2, we would be lucky to start with two vertices connected by an edge, but we must consider the worse case of two vertices not connected by an edge; in this case, we would need four vertices and six edges, for a total of W(2) = 4*2 + 6 = 14. Similarly, for three nodes we would start with three unconnected vertices, so we'd need three vertices and six edges to get to C, meaning W(3) = 3*2 + 6 = 12.
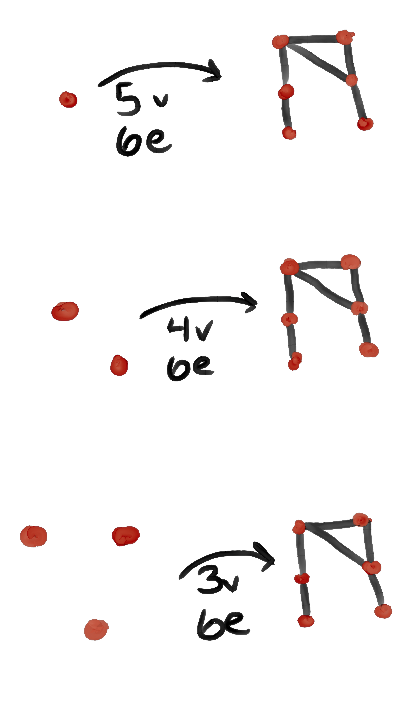
To recap, we have
W(1) = 16
W(2) = 14
W(3) = 12
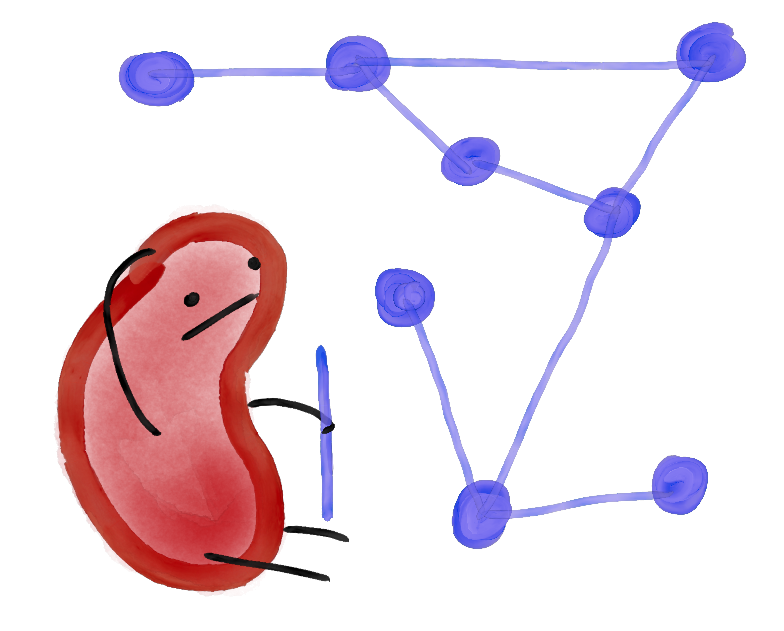
With n = 4, things get more interesting. We can notice that if we start with four unconnected vertices, we'll need only two vertices and six edges to get to C, giving us W(4) = 10. But, since our goal is to find the worst possible starting graph with four vertices, we can perhaps look for a graph that isn't a subgraph of the eight six-vertex asymmetric graphs above. The only such graph with four vertices is the complete graph K₄. Here's where things get tricky: starting with K₄, what's the best possible score?
Because K₄ is not a subgraph of any of the asymmetric graphs above, we know we must have at least seven vertices, so let's go ahead and add the three more we need. Now our goal is to connect these three vertices to the K₄ with the fewest amount of edges. Well, we clearly can't use fewer than three edges, since if we could, we might as well not use one of the added vertices. We'll first notice something critical:
Here, 'interacting uniquely' means that we need to add an edge to each starting vertex, connecting it with some unique subgraph. For example, we can try adding the three nodes to our K₄ without interacting with all but one starting vertices:
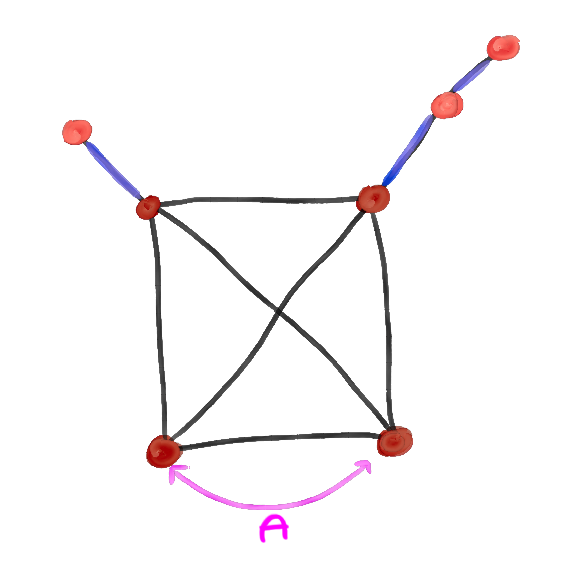
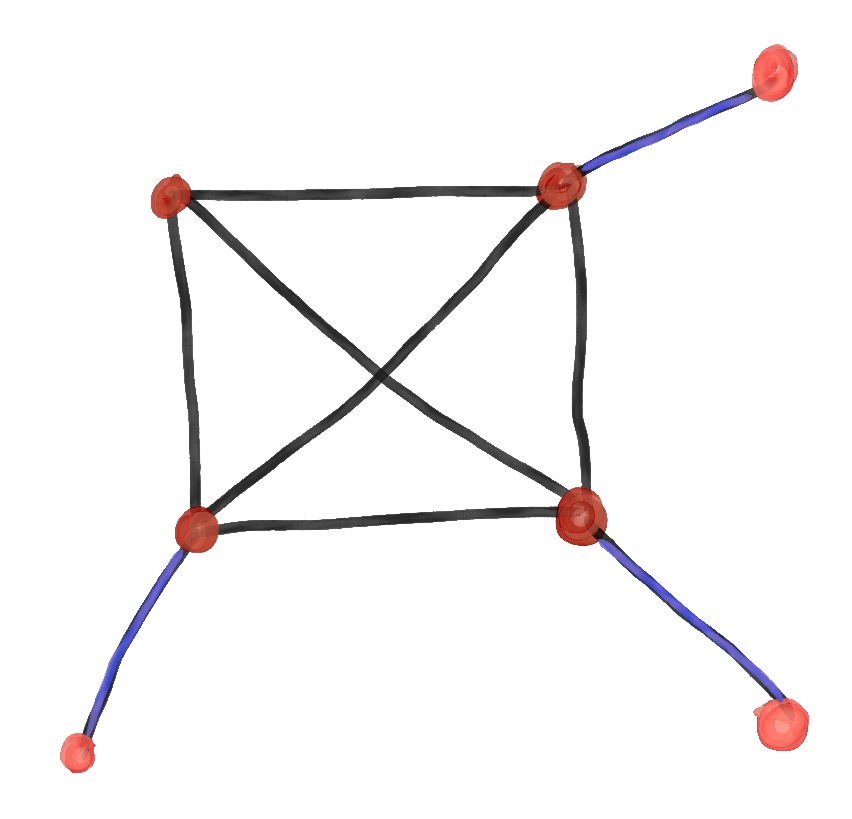
Here, we can see we at least need to add a fourth edge. Doing so allows us to make this configuration:
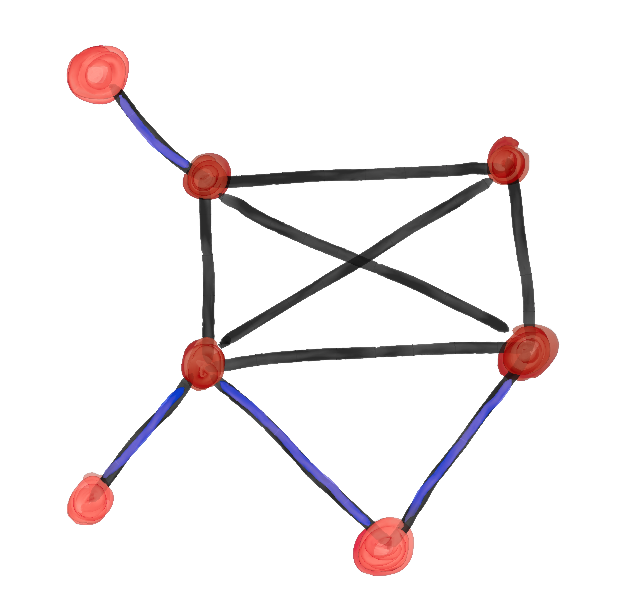
Before we go to five vertices, we naturally notice a pattern. Starting with zero vertices and going up, we have scores of 18, 16, 14, 12, and 10 for n from 0 to 4. It becomes really tempting to say W(n) = 18 - 2n. Let's see how long we can maintain this model...
For a starting graph of five vertices, we first have to ask what the worst possible starting graph is. Starting with 5 unconnected vertices is actually kind of nice, since we're only one vertex and six edges from C, so a score of 8. So we'll consider the other extreme: the complete graph K₅. Should we consider K₅ minus any edges, since this might be as hard as solving K₅ but in the end will need one extra edge? Well, at least in this case, it seems like no; removing an edge would make it closer to solving the K₄. So, let's find the best score for K₅.
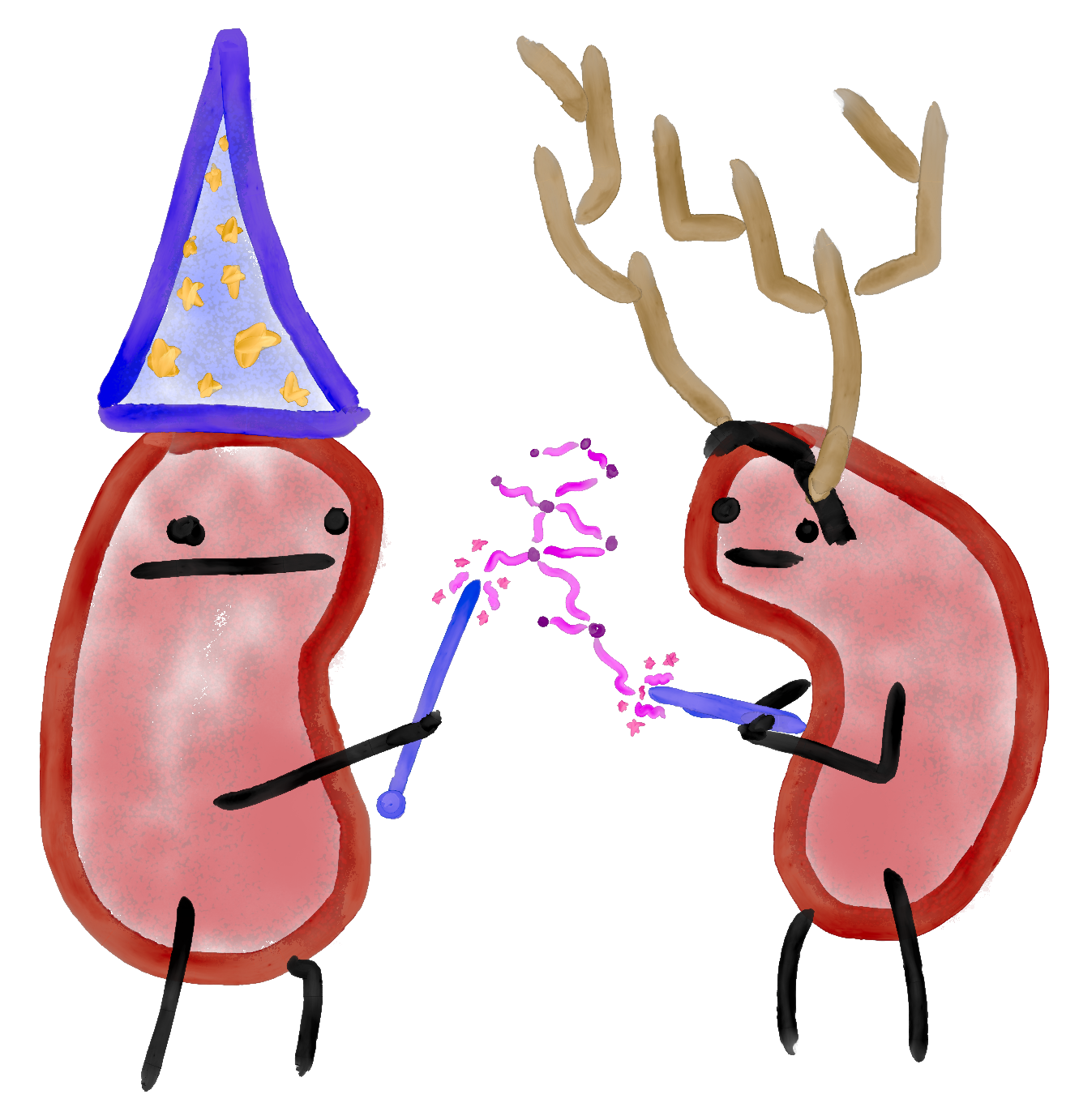
It's actually pretty hard to find the best score, so let's first find a way to anisocrate it with a decent score. One way to do this is with what I call the Tall Hat Method. I picture in my head a party of wizards standing around a magical pentagramal carving in the floor, preparing some kind of ritualistic spell or something. These wizards are pretty petty, though, and like to outclass each other by wearing a taller hat than their neighbor. It looks like this:
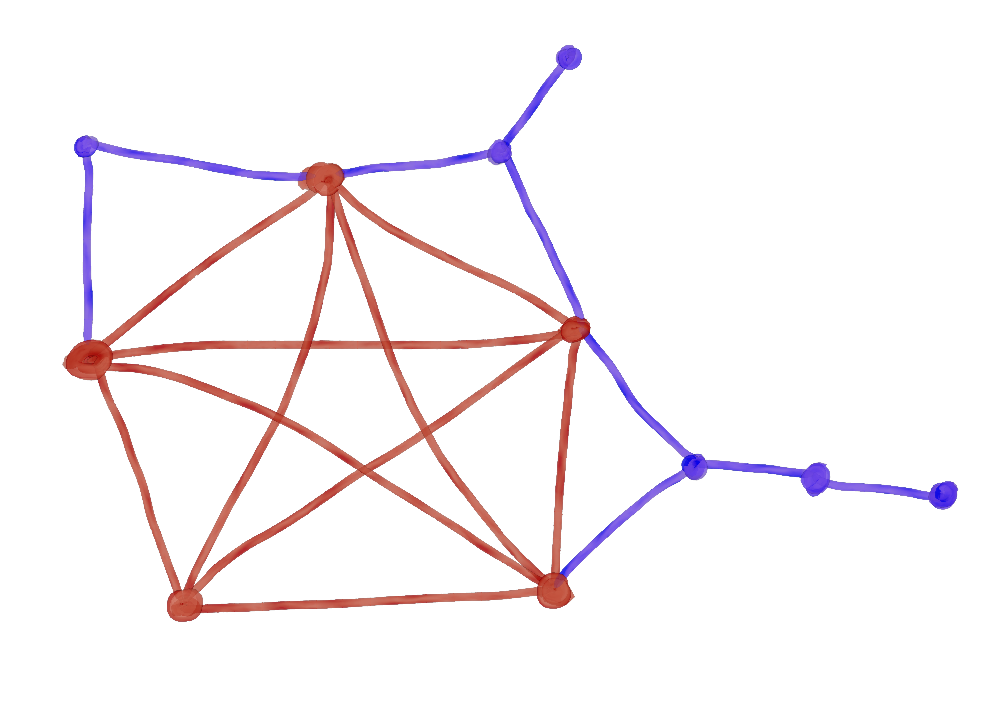
It's clear that no hat is isomorphic to any other hat, which means that the original vertices can no longer
permute, and we made sure to not add any symmetry. Without a solid proof, we'll claim that this method of
adding vertices and edges does break all symmetries. This means that for any complete graph (with four or
more vertices), we can anisocrate it with tall hats. We can
do this on K₄ and notice that, needing only two hats, we have three added vertices and five added
edges, making a score of 11. Not optimal, but not bad either. On our K₅, we only need three hats, so
that makes six added vertices and nine added edges for a score of 21. Indeed, we can continue this pattern
for any complete graph of n vertices, noticing that the kth hat has a score of 3k + 1
and doing some algebra to derive a formula:
Work
We notice that the \(h\)th hat gives a score of \(3h + 1\). Using the finite summation formula, we get
\begin{align} \frac{h(4 + 3h + 1)}{2} = \frac{3h^2 + 5h}{2} \end{align}
total points after \(h\) hats. Notice, though, that \(K_n\) only needs \(n-2\) hats, so we can plug in \(h =
n-2\) to get
\begin{align} \frac{3(n-2)^2 + 5(n-2)}{2} &= \frac{3(n^2 - 4n + 4) + 5n - 10}{2}\\
&= \frac{3n^2 - 12n + 12 + 5n - 10}{2}\\
&= \frac{3n^2 - 7n + 2}{2}.
\end{align}
So, for any complete graph of n vertices, we can say that we can at least get a score of \(\frac{3n^2 - 7n + 2}{2}\).
What I'm about to do is kind of ill-mannered, devious, and vile. I want to make an assumption, without proof, about graphs, so that working with our W(n) function is a bit easier. It's a pretty believable assumption to me, but I'll make it clear when I use it and what the alternative would be if it were false.
Assuming this, we can immediately start to bound W(n).
But I think we can do better. Perhaps we can stick with the hat idea, but consider whether or not we always
need to
add an extra vertex to make a new hat. That is, can we make nonisomorphic hats with the same number of
vertices? Yes! I call this the Antler Hat Method, imagining that during the holiday season, the wizards
festively meet for their magic circle after turning their hats into reindeer antlers. We can partition the
nodes on a hat into two antlers in \(\lceil\frac{n}{2}\rceil\) distinct ways.
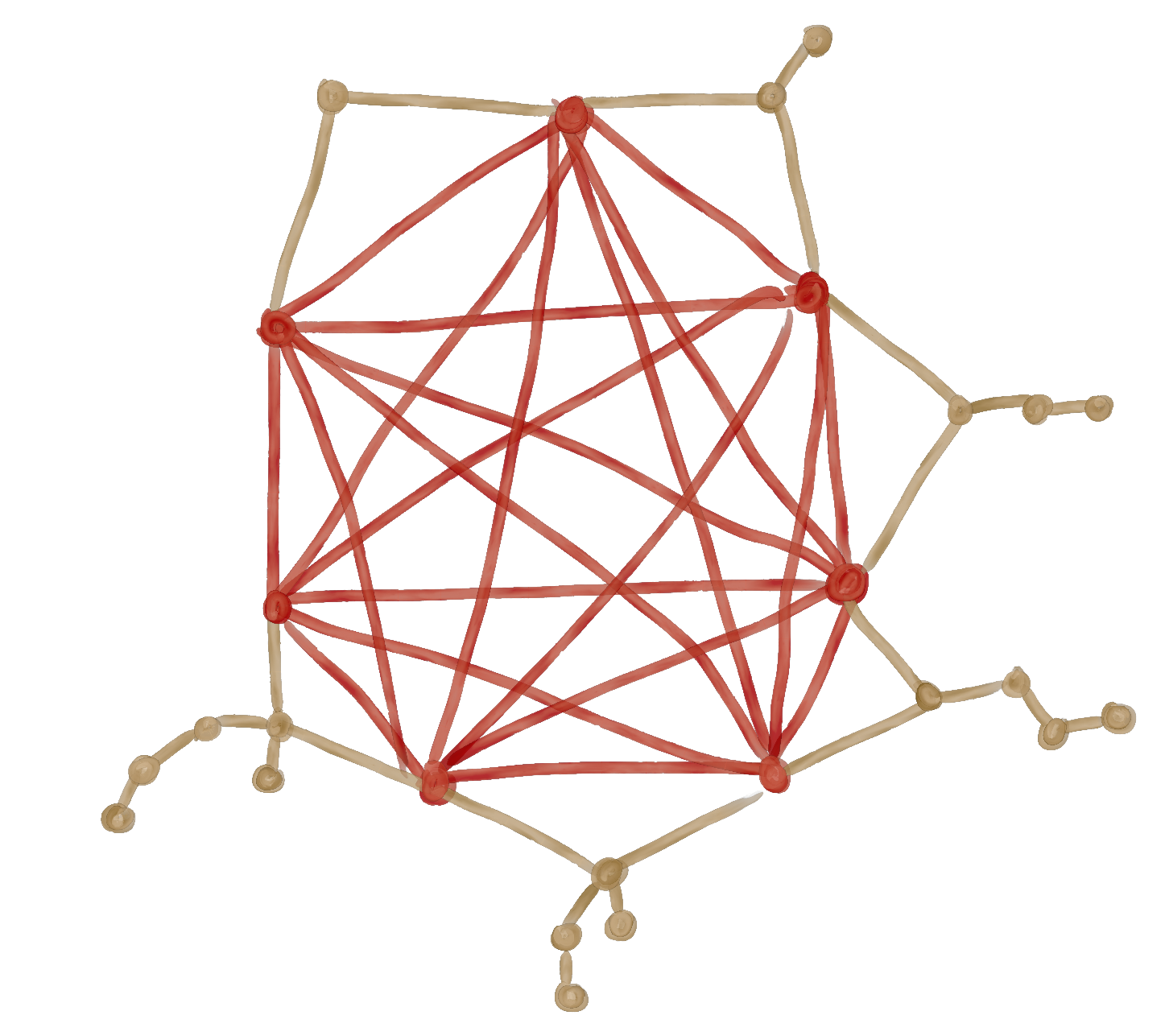
| Hats h | Vertices of hth Hat | Edges of hth Hat | Score of hth Hat | Total Score |
|---|---|---|---|---|
| 1 | 1 | 2 | 4 | 4 |
| 2 | 2 | 3 | 7 | 11 |
| 3 | 3 | 4 | 10 | 21 |
| 4 | 4 | 5 | 13 | 34 |
| 5 | 4 | 5 | 13 | 47 |
| 6 | 5 | 6 | 16 | 63 |
| 7 | 5 | 6 | 16 | 79 |
| 8 | 6 | 7 | 19 | 98 |
| 9 | 6 | 7 | 19 | 117 |
| 10 | 6 | 7 | 19 | 136 |
| 11 | 7 | 8 | 22 | 158 |
| ... | ... | ... | ... | ... |
Things don't actually improve until K₇; the Tall Hat Method gives us a score of 50 whereas the Antler Hat Method gives us a score of 47. A difference of 3 isn't great but it's not negligible. Because this new method, in a sense, recycles hats more and more as n increases, the Antler Hat Method far outpaces the Tall Hat Method for, say, n = 1,000,000,000.
Yet, we can probably still do better. The Antler Hat Method only uses two antlers, but if we used more antlers, we can keep conserving resources, at least when possible. We might call this the Partition Hat Method, because it depends on the number of partitions of the number of nodes. For that matter, we don't even need to just use antlers, we can connect our antlers in unique ways to save on resources. We might call this the Party Hat Method, because we're looking for unique asymmetric hats that have no certain form. And who says we need a new hat for each wizard? Perhaps if we arrange the hats in a certain way, we can reuse old ones. But wait, does each wizard need a hat, or can some wizards maybe share a hat? Okay...it's starting to get really hard to find an optimal algorithm or method to solving complete graphs. Maybe we can shift our focus to other types of graphs.
Cycles
Whereas with the complete graphs, finding an optimal strategy got more and more difficult, with cycles
things are really nice. We can prove that for any cycle with six or more vertices, the best score is
always 2. Recall that there are no asymmetric graphs with five or fewer vertices, so this only holds for
cycles with more than five vertices.
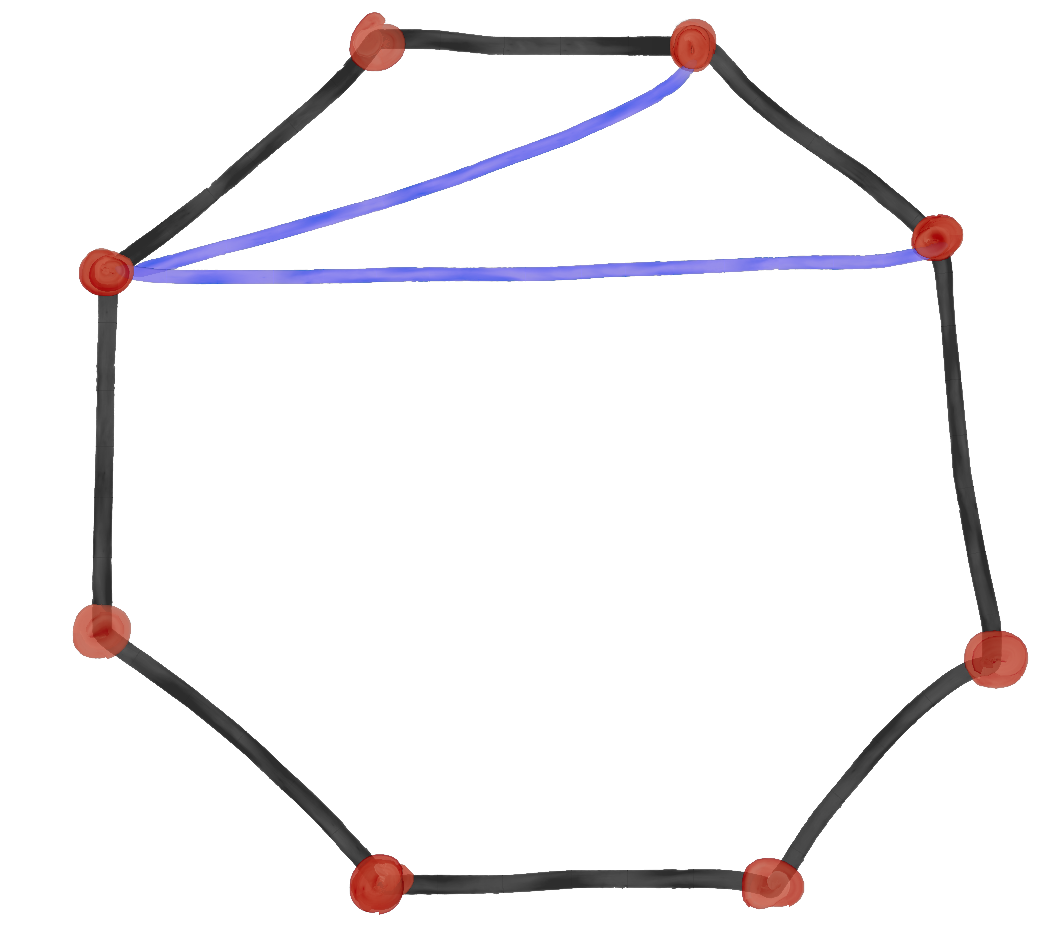
Proof.
We'll first want to show that no cycle has a best score of 1, i.e. adding an edge won't make a graph asymmetric. Well, if such an edge connected v and w, then there would be an automorphism that moves v to w and w to v (think reflectional symmetry still exists in the graph).We can now show a two-move strategy that always works on cycles. Consider some node v, and call the node two places to the right v+2 and the one three places to the right v+3. Connecting an edge from v to v+2 and an edge from v to v+3 creates an asymmetric graph. To prove this, suppose there existed some automorphism A of this graph. Notice that v has degree 4, v+2 and v+3 both have degree 3, and all else has degree 2. By nature of automorphisms, A(v) = v (A must fix v), since there is no other vertex of degree 4. Now, A must either fix v+2 and v+3, or swap them. If A doesn't fix them, then we can see that distance between v+2 and v is 2, while the distance between v+3 and v is 3 from one direction and at least 3 in the other direction. Since automorphisms preserve distance between vertices and fixed points, this isn't possible. If A fixed v+2 and v+3, then we can see that all other nodes must be fixed, and we're left with the trivial automorphism. Thus, the only possible automorphism is the trivial automorphism, and the graph is asymmetric. \(\Box\)
Complete Balanced Binary Trees
Complete balanced binary trees (BBTs or perefect binary trees) are an interesting specimen here. They are both super simple structures and rich in symmetry. With just the fifth tree, which has \(2^5 - 1 = 31\) vertices, we get a whopping 32,768 automorphisms! Intuitively, at least for me, the simple structure and rich symmetry conflicted, so I didn't know what to expect in terms of best possible score. But we can notice something crucial: we kind of only have to worry about the leaf nodes. And actually only every pair of leaf nodes. That is, if we don't add an edge to a leaf node or add an edge to its sibling, then an automorphism exists that just swaps that leaf node with its sibling. Let's call \(\gamma_n\) the lowest possible score for a balanced binary tree with \(2^n-1\) nodes. Then \(\gamma_n\) is at least a quarter of the number of leaf nodes (the number of edges it would take to make sure each leaf or its sibling has an added edge). Well, this is just \(2^{n-2}/2 = 2^{n-3}\). So \(2^{n-3} \leq \gamma_n\).
Here is a strategy for guaranteeing \(\gamma_n \leq 2^{n-2}-1\):
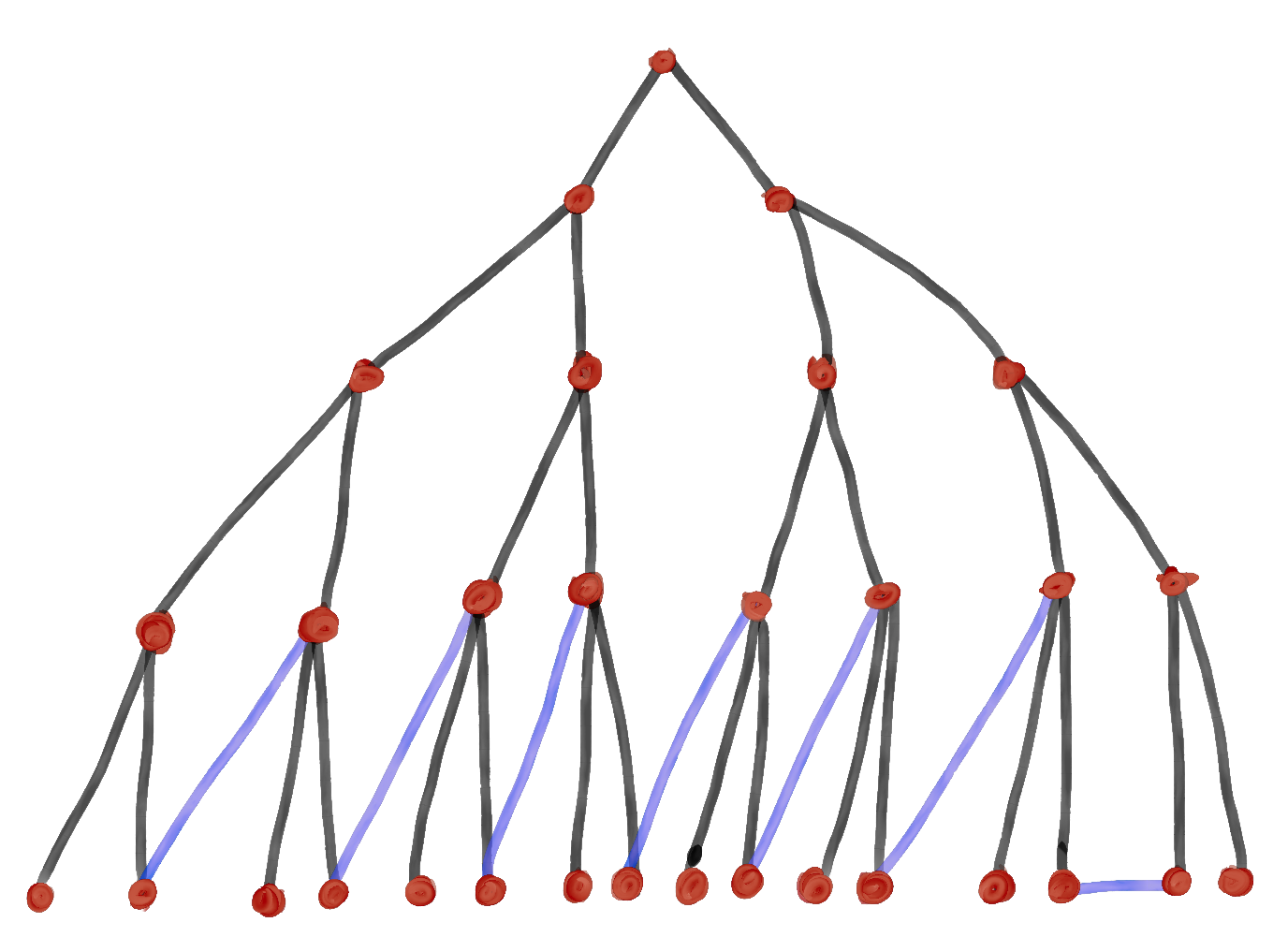
So, we have our score bounded by \(2^{n-3} \leq \gamma_n \leq 2^{n-2} - 1\). But consider the following strategy:
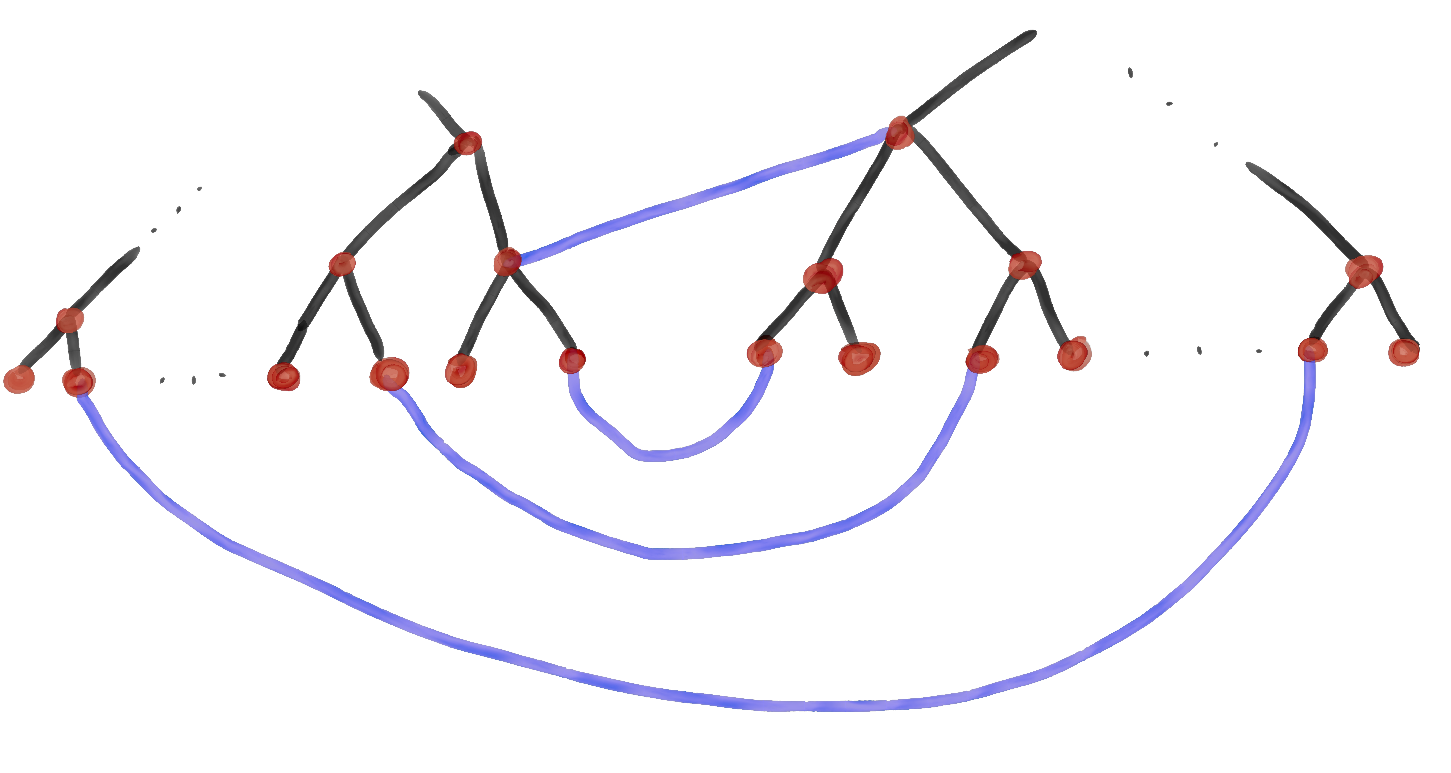
It seems visually clear that this should always work, so I'll forgo a proof, perhaps writing it up at a later time. But this means that \(\gamma_n = 2^{n-3} + 1\). And we can reason that we can't do any better than that, i.e., we can't anisocrate a balanced binary tree of \(2^n-1\) nodes in only \(2^{n-3}\) edges. Well, if this were the case, this would only be able to connect every pair of leaves to some other pair of leaves. You can check that we can always swap some nodes' children to yield an automorphism.
Kill Ratio
In studying balanced binary trees, we saw something really cool: the fifth BBT had 31 nodes and took only 5 edges to anisocrate. Amazingly, those 5 added edges killed 32,768 automorphisms! We can consider what I'll call the 'kill ratio' of that binary tree: the ratio between the number of starting automorphisms and least number of edges needed to anisocrate, \(\frac{32,768}{5} = 6,553.6\). What is the kill ratio for any BBT? And can we find a better kill ratio?
Firstly, what are we really looking for? Let's define the kill ratio of a graph G as \(R_G = \frac{|Aut(G)|}{\lambda_G}\), where \(\lambda_G\) is the best possible isocration score. For reasons explained here, the number of automorphisms of a BBT with \(2^n-1\) nodes is \(2^{2^{n-1}-1}\). Combining that with what we found in the last section, we get a function that describes the kill ratio of a BBT with \(2^n-1\) nodes: \begin{align}R_{\text{BBT}_n} = \frac{2^{2^{n-1}-1}}{2^{n-3}+1}.\end{align}
This function grows really fast, so the larger the BBT, the greater the kill ratio. And that's really cool, because you can have so many automorphisms broken with so few edges. In other words, symmetry is fragile.
So what about other types of graphs? We saw that cycle graphs (for \(n>5\)) can always be anisocrated in two edges. For some \(n\), an \(n\)-cycle has \(2n\) automorphisms, so \begin{align}R_{n\text{-cycle}} = \frac{2n}{2} = n.\end{align} This is really nice! It's kind of a linear baseline for comparing other kill ratios. For now, let's look at only those graphs that can be optimally anisocrated with just new edges. How do other graphs compare?
Archipelagos
We'll look at the kill ratio of graphs of n vertices with no edges, what I like to call archipelagos.
When \(n>6\) we have an easy strategy to always ensure a score of \(n-1\) (for \(6 < n <1 5\), I
think this is optimal). We can simply form a graph of the form:
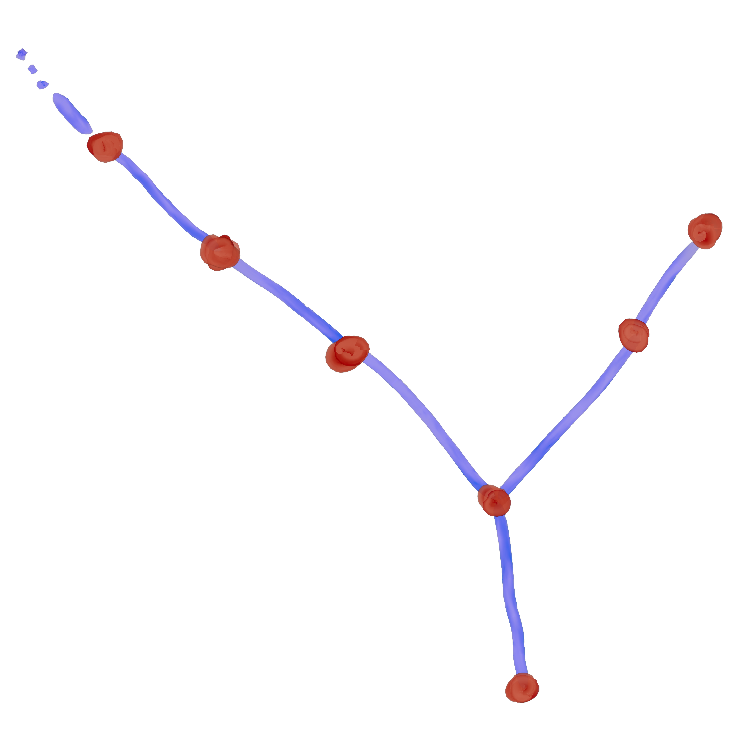
This isn't optimal for \(n\geq 15\), though, since we can make one of these graphs with 7 vertices and one of these graphs with 8 vertices, saving us an edge. Let's focus on the unoptimal \(n-1\), since that extra edge hopefully won't affect us too much. So, how many automorphisms are there of an n-chipelago? Well, the vertices are allowed to permute freely, so there are \(n!\) combinations. That gives us a kill ratio of \begin{align}R_{n\text{-chipelago}} = \frac{n!}{n-1} = n\cdot(n-2)!\end{align}
This kill ratio is the best yet!
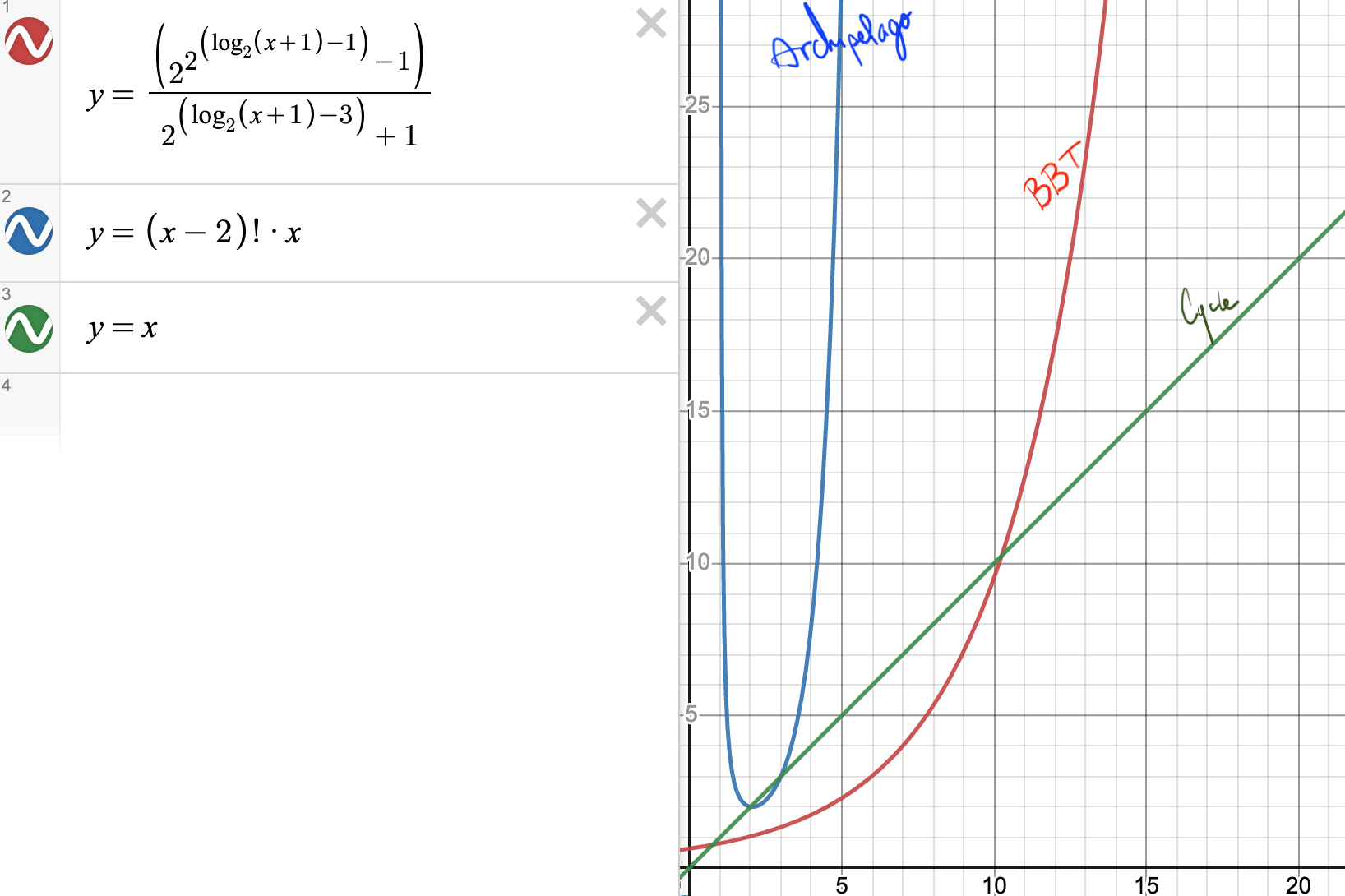
I think that maybe probably possibly any other family of graphs have kill ratios between these cycles and archipelagos. A 'family of graphs' is kind of non-rigorous term, so let's just say it's a set of 'similar' graphs that has only one graph of n vertices for any number n, up to isomorphism. This way, we're able to push the non-rigor from 'family' to 'similar'.
Summary and Open Questions
We started with a dream of finding a function that takes in the number of starting nodes of a graph and tells us whether we could have done a better job anisocrating the graph or not in hopes of being a better NAP player. We called this function W(n) and found the upper bound \begin{align}W(n) \leq\frac{3n^2 - 7n + 2}{2}\end{align} by analyzing complete graphs. So, for example, if we started with five nodes and scored 22, then we know we could've done better, since our bound says \(W(5)\leq21\). But we found ways to keep optimizing this strategy and shave off points. Describing functions for these strategies proved harder and harder, and showing one strategy was optimal felt even harder.
We moved on to solve more specific kinds of graphs. Cycles proved to be really easy, as we can always anisocrate them with two edges. BBTs are nice too, since we can also strictly use edges, and only use \(2^{n-3}+1\) edges. This made us curious about the starting-automorphism-count-to-optimal-anisocration-score ratio. This ratio is a sort of metric for measuring the fragility of a graph's symmetry. For cycles, it's really nice, since that ratio is equal to how many nodes are in the cycle. The BBTs have a pretty good one; its exponential growth shows that its symmetry is very fragile. We then saw that a group of unconnected vertices, which we called archipelagos, had an extremely steep kill ratio function.
I'm still very curious about this game. Aesthetically, the notion of optimally adding to a graph to break all its symmetries is beautiful and fun and tells us a lot about symmetry. In practice, I think it's just really fun. And in practicality, I think studying this asymmetry may have some implication in group theory by way of Frucht's Theorem, which I'll write about in the future. The asymmetry of graphs is also important in logic trees and SAT solvers in formal methods. All in all, studying the symmetry and asymmetry of this game and these graphs lead to very interesting things and leave me with many questions...
I would love to receive ideas, proofs, counterexamples, mistakes, etc. on any of the topics here, especially
Conjecture 1 and Conjecture 2, as well as better or even optimal strategies for
anisocrating complete graphs, a function that more accurately describes optimal anisocration of
archipelagos, and definitely a tighter bound on W(n). You can send any of this and more to my email:
ian [at] beanway [dot] me.
