This post is about a computer experiment; the code can be found here.
An interesting and natural question surrounding geometric triangulations of hyperbolic 3-manifolds is: for a fixed manifold
For the figure-8 knot complement, Dadd and Duan show that there are infinitely many! Their technique involves showing that the canonical triangulation admits a certain substructure along with a (sequence of) local move(s) on the substructure which, when applied, produces a new geometric triangulation containing the substructure. I call such a substructure a recursion gadget.
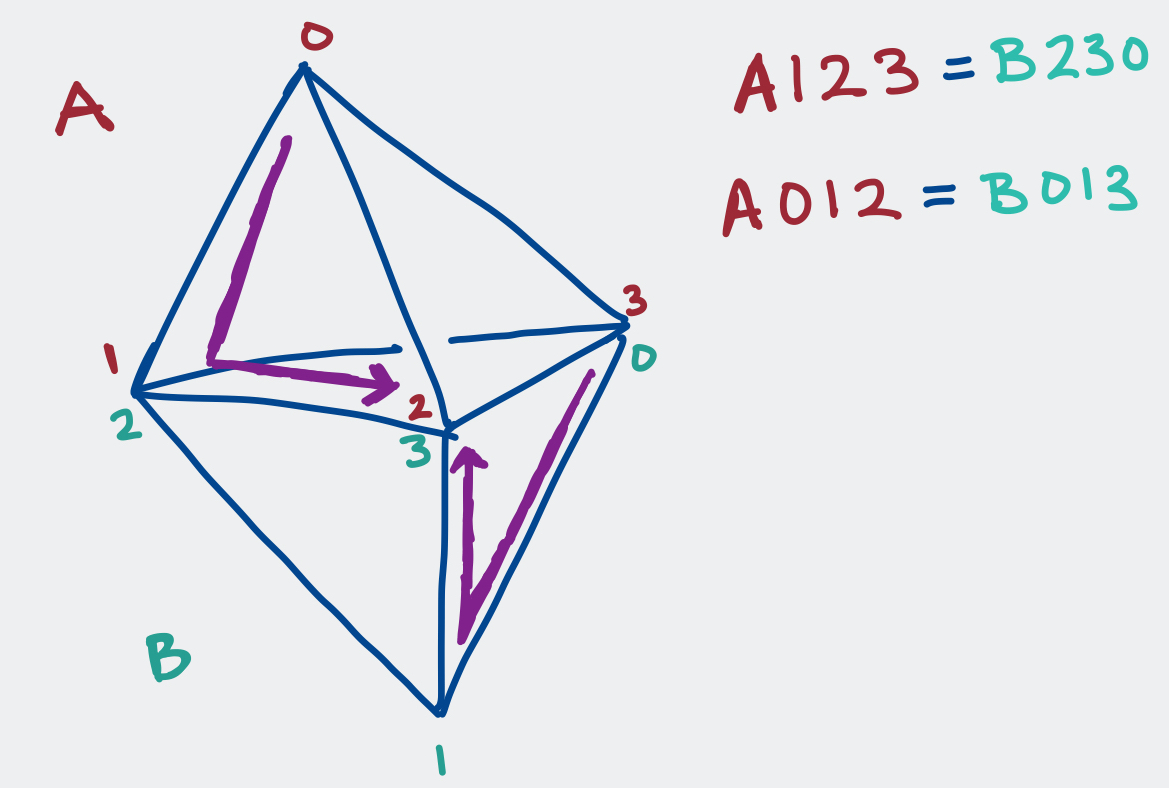
The recursion gadget found by Dadd and Duan, which I'll call the DD-gadget, is the following two tetrahedra sharing two faces:

If this is all that is required, then an easy next step is to see which manifolds have triangulations with a DD-gadget (after all, having infinitely many geometric triangulations is a property of the manifold). I wrote code to do exactly this, which now sits in the repository for my geometric moves code, here.
I ran this first on many census manifolds, and indeed many have this recursion gadget; I was able to find a gadget in 100 out of the first 270 manifolds in Snappy's Orientable Cusped Census, searching at a depth of 8 tetrahedra -- one was found about 37% of the time. But running it on Snappy's Census Knots yielded an even more surprising result. Out of the 1267 knot complements in this census, at least 1166 have some triangulation with a DD-gadget. That's over 92%.
Here's the idea: for each census triangulation, search the pseudogeometric subgraph of the flip graph containing the census triangulation. If ever you reach a triangulation five tetrahedra greater than the census triangulation, terminate the search. BFS through this graph until you find a DD-gadget, or until you've searched so far that the only possible 2-3 moves give a triangulation with five more tetrahedra than the starting triangulation.
Because the search terminates after an added height of five tetrahedra, the 101 manifolds for which no DD-gadget was found might still have infinitely many geometric triangulations. Increasing the search depth may or may not find a gadget.
If so many manifolds have this DD-gadget, what does that say about those that don't? If they have infinitely many geometric triangulations, does that imply they have some other gadget? And if they have finitely many...how does one prove that? From vastly searching the essential subgraphs of m003 (Figure-8 sibling manifold) and m017, it seems very believable that these have finitely many geometric triangulations.