Topological Proofs of Stuff and Things

I'm writing this page to serve as a collection of proofs I come across which use topological methods to show things about non-topological-like things. I'll update this page as I come across them. I find it interesting how topological methods are useful outside of its own discipline, or, from a different perspective, how topology lives in a lot of nonobvious places.

Infinite Primes

This proof of a classic theorem was invented by Hillel Furstenberg in the 1950s.°

Theorem 1. There are infinitely many primes.

Proof. Define $S (a, b)$ to be the arithmetic sequence ${a n + b : n \in N}$ . Then we can define a topology on $Z$ by calling a subset open if and only if it is the union of some arithmetic sequences. It is easy enough to show that this actually does define a topology on $Z$ . We notice two things:

The compliment of a finite set can't be closed, because this would imply that a finite set could be open. But the only finite open set in our topology is the empty set.
Any arithmetic sequence $S (a, b)$ is closed, since we can write the compliment of $S (a, b)$ as $⋃_{i = 1}^{a - 1} S (a, b + i),$ which is open because it is the union of arithmetic sequences.

Now suppose for the sake of contradiction that there were finitely many primes, indexed

p_{i}

. Since any integer can be written as the multiples of some primes, except for

{- 1, 1}

, we can write

Z ∖ {- 1, 1} = ⋃_{p_{i}} S (p_{i}, 0) .

Note that the left hand side isn't closed by our first bullet-point observation. But the right hand side, being the union of finitely many closed sets, must be closed (this isn't necessarily true for infinite unions of closed sets). This is a contradiction.

◻

Fundamental Theorem of Algebra

This is a classic application of the fundamental group. I'll assume that one has already calculated the fundamental group of a circle to be $Z$ , even though this takes a lot of work. I won't go into rigorous detail, but the point will be more to get a visual understanding of the proof.

Theorem 2. A degree $n$ -polynomial with complex coefficients $p \in C [x]$ has $n$ roots in $C$ .

Proof. If we show that one root of $p$ exists, say $α$ , then we can factor out $p (x) / (x - α)$ to get another polynomial in $C$ . So by some inductive argument, it suffices to show that a non-constant polynomial has a root in $C$ .

Suppose for the sake of contradiction that $p$ has no root in $C$ . So $p$ is a function from $C$ to $C ∖ {0}$ . We'll visualize the input and output spaces as follows:

Consider the circle around the origin $C_{r} = {r e^{i θ} | θ \in [0, 2 π)} .$ First, if the circle has radius 0, then $C_{0} = 0$ . So $p (C_{0})$ is some point in the output space:

Next, recall that when $x$ gets large, $p (x)$ starts to look like its highest order term. So if $p (x) = a_{n} x^{n} + \dots + a_{1} x + a_{0}$ , then at large values of $x$ , $p (x)$ acts like $a_{n} x^{n}$ (in an informal, handwavy manner of speaking). So for $r >> 0$ , we get that $p (C_{r})$ looks like $a_{n} (C_{r})^{n}$ , i.e. a big circle. So we should be able to find a value $R$ large enough so that $p (C_{R})$ encircles $p (C_{0})$ and the point $0$ .

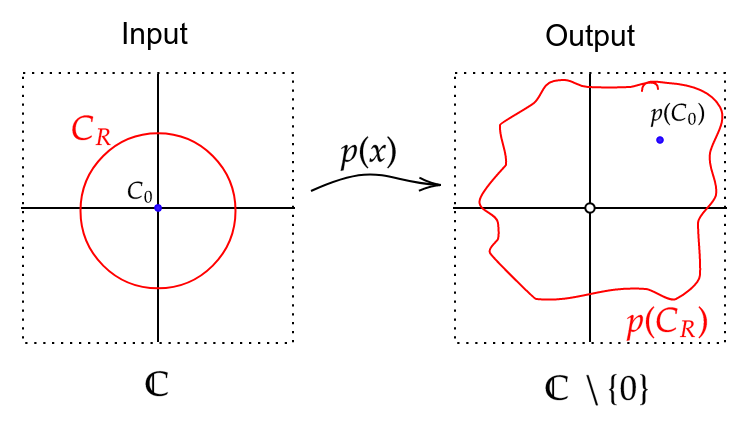
take C_R to a circular thing in the output

Finally, observe that varying $r$ from $0$ to $R$ defines a homotopy from $p (C_{R})$ to $p (C_{0})$ , because polynomials are continuous. But this means that the (loop homeomorphic to the) circle $p (C_{R})$ contracts to the point $p (C_{0})$ . The one-point-complement of $C$ is homotopy equivalent to $S^{1}$ , which has nontrivial fundamental group, and in particular $p (C_{R})$ describes a nontrivial element of this fundamental group, so this is a contradiction. In other words, we want to shrink the red curve $p (C_{R})$ to the blue point $p (C_{0})$ , but analysis of $S^{1}$ says that we can't do so without 'getting stuck' on the point 0. So $p$ must have a root in $C$ . $◻$