Learning Lean 4 Metaprogramming
There's a famous statistical argument that goes along the lines of, "A monkey seated at a typewriter bashing keys at random will, given enough time, churn out the complete works of Shakespeare." I want to formulate a special case of this argument: "An undergraduate seated at a type checker will, given maybe a Saturday afternoon, churn out the proof to a biconditional." -me, after spending a Saturday afternoon banging on my keyboard with Lean open
28-02-2022
Introduction
A few weeks ago I set out to learn the framework and practice behind metaprogramming in Lean 4. I've worked and studied Lean 3's metaprogramming features for a bit — albiet shallowly. But I understand the important concepts behind Lean 3's metaprogramming interface. In the upgrade to Lean 4, many things have changed. As of February 2022, the documentation for the changes, how to use them, and how to not get really really confused is slim. Because of this, most of my learning has been reading other tactics that have already been ported to Mathlib4, asking questions in the Zulip, and frantically and frustratingly playing around with things in Lean 4 itself.
I'm chronicling my adventures through the hazy overgrowth of what I imagine will be an arduous trek to a wonderful destination — the genius behind Lean 4. I hope these writings will help others who are trying to learn Lean 4's metaprogramming, and perhaps guide me towards writing a basic tutorial for writing tactics.
Documentation and Mathlib4
Since Lean 4 is so new, it's only natural that its documentation is thin. As of now, if someone wants to take up learning tactic-writing, they'll be met with only a few resources: a couple of really nice, but top-down-approaching, talks on YouTube; the skeleton of documentation on the Lean 4 docs; some amazing posts from the lovely people on the Lean Zulip; and Mathlib4 itself. Mathlib4 is an ongoing port (or rather, an experimental pre-port) from Lean 3's Mathlib. Most of the tactics from Mathlib have yet to be ported to Mathlib4, so it's open season for porting — all of the stubs for yet-to-be-ported tactics can be found here.
Review of Big Lean 3 Metaprogramming Concepts
⬝Metaprogramming is done in the Lean language
⬝It's done in monadic programming with one type of monad: the Tactic Monad
⬝Tactics are defined with the meta keyword
⬝The character ` is the quotation character, and % is the antiquotation
What's Changed
⬝There are now many types of monads: Tactic Monad, MetaM Monad, IO Monad, TermElabM Monad
⬝Some syntax
⬝No more meta keyword
Where's Meta?
The keyword meta formerly esured safety in recursive procedures and allowed us to define meta programs. For safety, we now have the `unsafe` keyword.
-- Lean 3
-- needs `meta` because Lean doesn't know
-- how to prove this recursion terminates
meta def collatz : ℕ → ℕ :=
fun | n => if n = 1 then 1
else if n%2 = 0 then collatz (n/2)
else collatz (3*n + 1)
-- Lean 4
-- needs `unsafe` because Lean doesn't know
-- how to prove this recursion terminates
unsafe def collatz : Nat → Nat :=
fun | n => if n = 1 then 1
else if n%2 = 0 then collatz (n/2)
else collatz (3*n + 1)
For defining tactics, we have five new keywords:
⬝syntax: defines the syntax of a tactic
syntax (name := myTactic) "myTactic" ident (" : " term)? : tactic
-- declares the syntax of myTactic to be `myTactic a` or `myTactic a : t`
-- so myTactic takes in some identifier, and optionally its type
⬝macro_rules: defines a macro for a given syntax. Works as a syntax-to-syntax translation
macro_rules
|`(tactic| myTactic $i:ident) => `(tactic| repeat apply trace "hi")
|`(tactic| myTactic $i:ident : $t:term) => `(tactic| repeat apply trace "hi with type!")
-- notice the powerful syntax matching
⬝macro: shorthand for combining syntax and macro_rules
⬝elab_rules: for getting your hands dirty. Works for tactics that mess with the context, goals, etc. (examples below)
⬝elab: shorthand for combining syntax and elab_rules
Let's compare two tactics
Perhaps it's best to see the changes via a comparison of old versus new. Let's compare the Mathlib (3) version of swap and the Mathlib 4 version of swap.
In both versions, this tactic swaps the first goal with the second goal if there are at least two goals, or nothing otherwise. Notice that the Mathlib 4 tactic takes a more generalized approach. I'll rewrite it so that it's easier to see the syntactic differences:
-- Lean 3
meta def swap : tactic unit :=
do gs ← get_goals,
match gs with
| (g₁ :: g₂ :: rs) := set_goals (g₂ :: g₁ :: rs)
| e := skip
end
-- Lean 4
syntax (name := swap) "swap" : tactic
elab_rules : tactic
|`(tactic| swap) => do
let gs ← getGoals
match gs with
| (g₁::g₂::r) => setGoals (g₂::g₁::r)
| e => setGoals e
Notice the main syntax changes: meta is now syntax and elab_term; we use let to write to variables (for both ← and :=); a lot of tactics are camelcase now; matching uses (=>) instead of (:=); no more keyword end. It would be really really nice if porting tactics were as easy as making these syntactic changes. Unfortunately, this isn't so much the case.
Why is it harder than that?
As noted above in the mini change log, Lean 4 introduced many new monads into the metaprogramming universe. There are two main obstacles that I see when porting: having to juggle (and understand in the first place) the many types of monads, and dealing with the lack of resources in terms of examples, other tactics, and guides. To understand this better, consider how we might write set. In Mathlib (3)'s version, it's nothing too tricky. Consider if we just want to do set x := y for some y already in our contex. Then all we want to do is get the type of y, get the expression of y, and add x := y to our context. Then we can go through our context and change all instances of y with x.
But let's focus on the first part—adding to our context. It seems like it would be simple; afterall, in Mathlib (3) it's just a definev. Lean 4 has a similar define, but integrating it into a tactic is tricky. Here was my solution:
private def defineV (nm : Name) (tp : Expr) (tme : Expr) : TacticM Unit := do
liftMetaTactic1 fun mvarId => do
let h2 ← (define mvarId nm tp tme)
let (h, h2) ← intro1P h2
withMVarContext h2 do
return h2
With this, we can call defineV inside our tactic. As far as I could fine, there is no tactic that simply adds something to the context as easily as Lean 3's definev (or assert or whatever your favorite method was). Why can't we just plop define into our Lean 4 tactic? It comes back to the new monad types...
The Monad Zoo
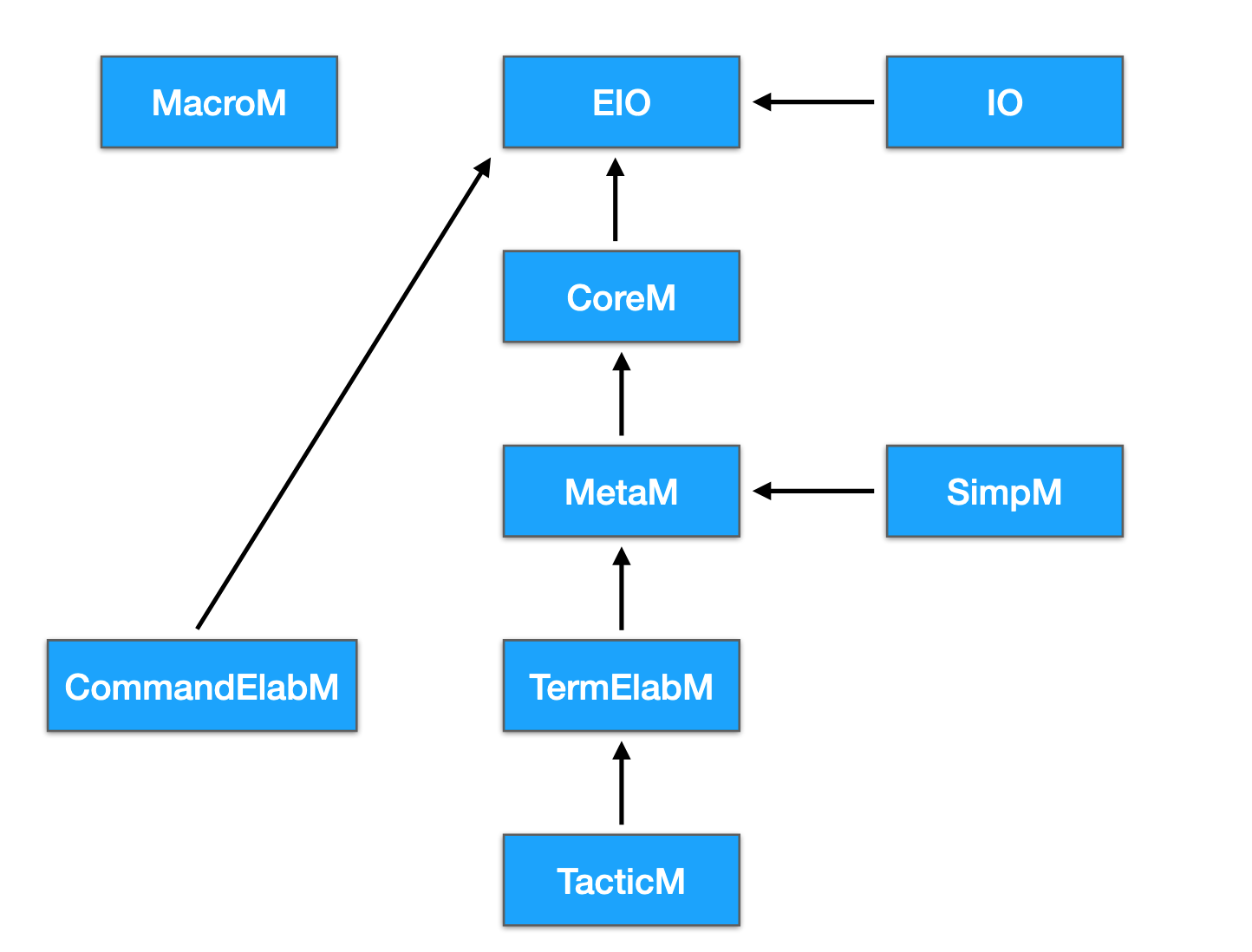
Perhaps it's more of a monad jungle, where it's humid and you have no idea where you are or are going and the lush vegitation obfuscates your view of anything and you get beaten up by gorillas and then eated by jaguires. Okay so it's not that bad. But coming to the partial understanding of how these monads work together was really new to me. My understanding is that while the new set of monads make metaprogramming cleaner, more abstractable, and more flexible, it makes learning how to do it much harder (at least for me).
Here is a picture of the "Monad Zoo":
So here, we'll focus on TacticM, TermElabM, and MetaM. So, inside elab_rules, we're using the type tactic. If we check out define, we see it's of type MVarId → Name → Expr → Expr → MetaM MVarId. So it's of type MetaM. So, we need to lift up define out of the "universe" of MetaM and into the "universe" of TacticM. That's exactly what liftMetaTactic1 does.
Tackling the above defineV line by line should prove to be informative.
private def defineV (nm : Name) (tp : Expr) (tme : Expr) : TacticM Unit := do
This tells us that our defineV function is of type TacticM Unit, so we're able to use it in our tactic!
liftMetaTactic1 fun mvarId => do
As just explained, liftMetaTactic1 lifts up our MetaM function into TacticM. If we go into the type of liftMetaTactic1, we see (MVarId → MetaM (Option MVarId)) → TacticM Unit. So, it takes in a function from MVarId to MetaM (Option MVarId). What does this mean? Well, goals are represented as metavariables (MVars). So, in other words, this takes in a function from goals to (option) goals. In particular, liftMetaTactic1 applies the input function to the main goal.
let h2 ← (define mvarId nm tp tme)
Here, we apply define. Our context should now have gone from Ctx |- target to Ctx |- let nm : tp := tme; target.
let (h, h2) ← intro1P h2
This introduces the let statement out of the goal.
withMVarContext h2 do
return h2
This returns the MVarId resulting from introducting the let statement from the line above.
20-03-2022
Hammering a Screw
It's important when thinking of how to write your tactics to keep your goal in mind. Constantly evaluating how to get to your goal is
even more important.
It's easy to get lost in some convoluted path to accomplish something simple. I found this out the hard way.
I was looking for a way to rewrite the names of variables in my set tactic. I traveled to a million different
preexisting files looking for a way to do this using change or some core-oriented methods. After writing a (somewhat)
complex defineV function, it was written in my mind that I needed a complicated use of change or something.
In reality, I just needed to rewrite the variable names. Rewrite. Rewrite...
evalTactic (← `(tactic| try rw [(id rfl : $pv = $a)] at *))
It was such a frustratingly simple solution. So remember to take a step back every once in a while and reevaluate whether what you're
doing is as complicated as it needs to be. Pick your tools right. Don't hammer a screw.