Triangulating Polygons

Triangles are pretty cool. Our goal is to take dumb polygons and make them cool by cutting them into triangles.

In particular, given some lattice polygon $P$ with four or more vertices, we want to find two lattice polygons with disjoint interiors whose union creates $P$. Notice by induction that finding such a method will yield a triangulation of $P$.

The motivation for the algorithm comes from the idea that between three adjacent vertices, we can connect the unconnected vertices to form a new triangle, so long as

1. the added edge lies within the interior of the polygon, and
2. the added edge doesn't overlap any existing edges.

So we can reduce our problem to the following pseudocode:

 # polygon is a list of vertices ordered so that element i is adjacent to element i+1    
 def triangulate(polygon):
     if (polygon.length < 4):
         return polygon
     for each adjacent v1, v2, v3 in polygon:
         l := line connecting v1 and v3;
         i := interior of triangle with vertices v1, v2, v3
         if (l is in interior && i does not contain any vertices of polygon):
             draw l;
             polygon.remove(v2);
             return triangulate(polygon) // recursive call on original
                                         // polygon minus the v2 that was cut out

        

Orientation

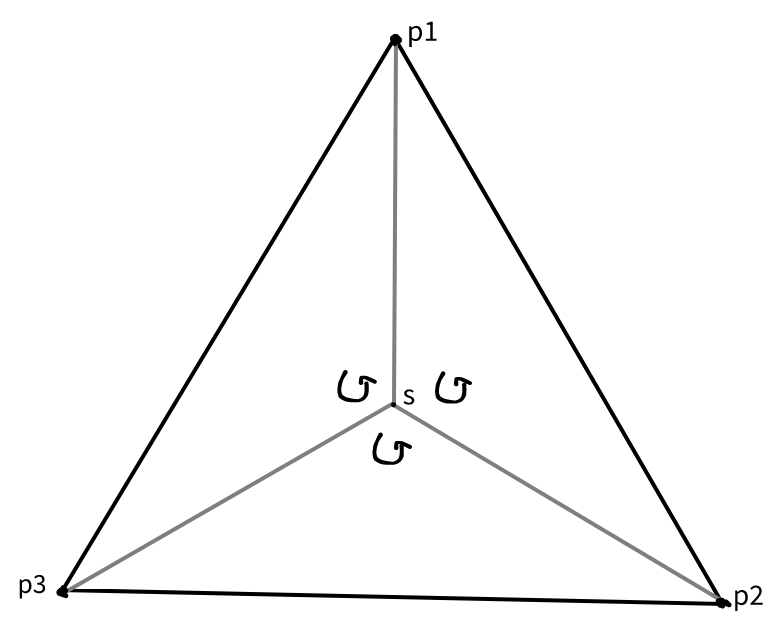
How can we check whether the new edge of three points forms a free triangle? We can use orientation! From now on we'll consider our input 'polygon' as really a list of vertices ordered counterclockwise such that element $i$ shares an edge with element $i+1$. If our list $V$ of vertices is ordered in such a way, we can check that any set of three elements indexed $i$, $i+1$, $i+2$ forms a triangle whose interior exists in the interior of $V$ if and only if the three elements are counterclockwise in order.

We can calculate the orientation of three points $(x_1,y_1)$, $(x_2,y_2)$, and $(x_3,y_3)$ by noticing that if the points are ordered counterclockwise then we want the slope of the second line relative to the first line to be greater than the slope of the first line, i.e., $$\frac{y_2-y_1}{x_2-x_1}<\frac{y_3-y_2}{x_3-x_2}.$$ Rearranging, we can find that the three points are ordered counterclockwise if and only if $$(y_3-y_2)(x_2-x_1)-(y_2-y_1)(x_3-x_2)>0.$$ It's worth noting that the points are collinear if the above equals 0 and clockwise oriented if less than 0.

So recall that we need to solve two problems:

1. How to tell whether the interior of a new triangle is in the interior of the whole polygon...
2. How to tell whether the new line created intersects any previously drawn edges...

Problem 1

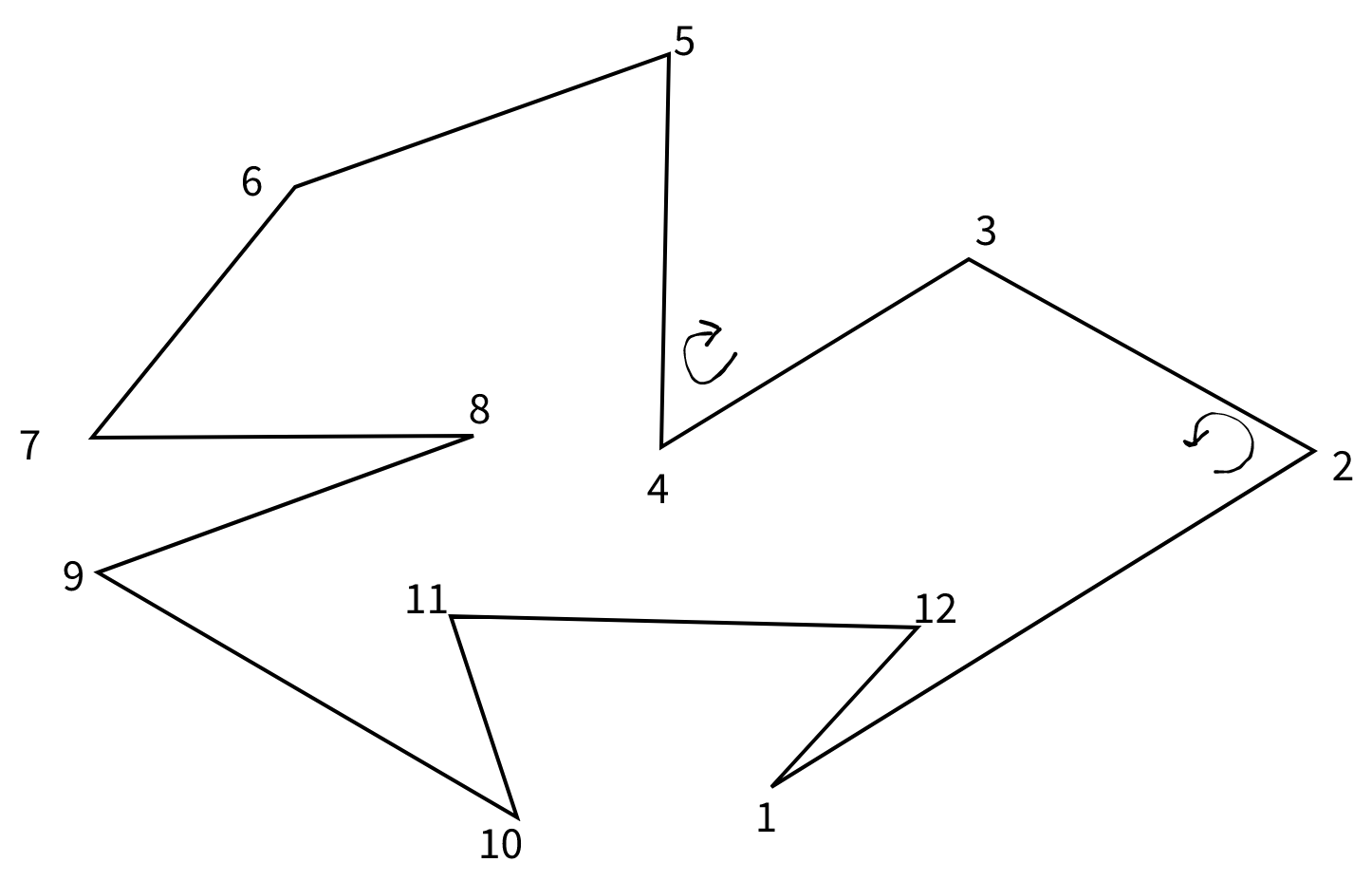
As stated before, the interior of the new triangle is in the interior of the whole polygon if and only if the points, when ordered properly, are counterclockwise oriented. This is best communicated by illustration:

Problem 2

So we want to make sure the new line we create doesn't intersect existing edges. For example in the polygon above, the triangle 1-2-3 is oriented counterclockwise, but if we drew the line 1-3, we would intersect another edge. So we should try to avoid that. But we can also just exploit the fact that we're working only with polygons, and notice that we would cross an edge if and only if some other point exists in the interior of the new triangle (in the example, 12 is that point). This is true because the polygons we are working with only have straight, non-intersecting edges.

There are many ways to do this, but we've already built up on a framework of orientation, so let's just use that! Take a triangle formed by $p_1$, $p_2$, and $p_3$. A point $s$ inside of the triangle will have the same orientation for $p_1\to s\to p_2$, $p_2\to s\to p_3$, and $p_3\to s\to p_1.$

Implementation

Algorithm

// Input: poly_points, a list of vertices of the polygon ordered
//        in ccw rotation starting from an arbitrary point
function triangulate(poly_points) {
    var p1, p2, p3;
    if (poly_points.length < 4) {return} // base case: triangle
    for (var i = 0; i < poly_points.length; i++) {
        // for each set of 3 adjacent vertices
        p1 = poly_points[i]
        p2 = poly_points[(i + 1) % poly_points.length]
        p3 = poly_points[(i + 2) % poly_points.length]
        if (ccw(p1, p2, p3) > 0 && clearShot(p1, p2, p3)) {
            // draw new line between p1 and p3
            line(p1[0], p1[1], p3[0], p3[1])
            // kill p2 and bury the body
            poly_points.splice(i + 1, 1)
            // recursively call on polygon with p2 removed
            return triangulate(poly_points)
        }
    }
}

/////////////// Helper Functions ///////////////
// Given 3 points, returns whether those points are
// oriented ccw (+), collinear (0), or cw(-)
function ccw(p1, p2, p3) {
    return (p2[0] - p1[0]) * (p3[1] - p1[1]) - 
        (p2[1] - p1[1]) * (p3[0] - p1[0])
}

// Given 3 numbers, returns whether they have the 
// same sign
function sameSign(a, b, c) {
    return (a * b > 0 && b * c > 0)
}

// Given a point and a triangle, returns whether the point 
// is in the interior of the triangle
function inTriangle(s, p1, p2, p3) {
    return sameSign(ccw(p1, s, p2), ccw(p2, s, p3), ccw(p3, s, p1))
}

// Checks whether the line between p1 and p3 can be drawn
// by checking if any points exist in the interior of 
// the triangle formed by p1 p2 and p3
function clearShot(p1, p2, p3) {
    for (var j = 0; j < points.length; j++) {
        s = points[j]
        if (inTriangle(s, p1, p2, p3)) {
            return false
        }

    }
    return true
}