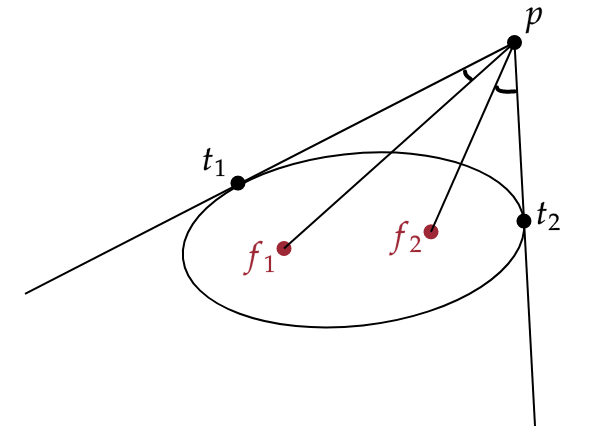The Steiner Inellipse

It's easy to see that the root of the derivative of a quadratic is the midpoint of the roots of the quadratic: Let \(p(x) = (x-\alpha)(x-\beta)\). Then \(p'(x) = (x-\alpha) + (x-\beta)\). So setting \(p'(x) := 0\), we get \(x = \frac{\alpha + \beta}{2}\).

But what happens when we have a cubic? Do its two roots follow a similar even distribution? Here I will show a theorem, due to Marden, showing that the roots of a cubic have a nice geometric property.

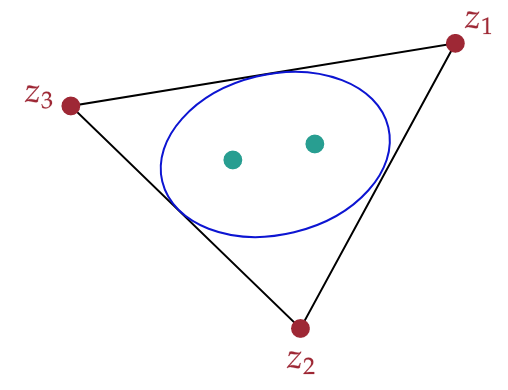
Theorem. Let \(p(x) \in \mathbb{C}[x]\) be a cubic polynomial with roots \(z_1\), \(z_2\), and \(z_3\). Then the roots of the derivative \(p'(x)\) are exactly the focii of an ellipse which is tangent to the midpoints of the line segments \(z_1z_2\), \(z_2z_3\), and \(z_3z_1\). This ellipse is known as the Steiner Inellipse.

The proof I'll show here is an adaptation of Dan Kalman's proof, (which is an amalgamation of proofs by Marden [from 1929] and Bocher [from 1892], although the first proof seems to be attributed to Siebeck [from 1864]). To begin we'll state a few facts that we'll need. If you're not convinced of any of these facts, I prove them out of the way; see their adjacent links.

Facts:

1. Let \(M\::\:\mathbb{C}\to\mathbb{C}\) be a linear transformation and let \(p(z) = (z-z_1)(z-z_2)(z-z_3)\). Define $$p_M(z) = (z-M(z_1))(z-M(z_2))(z-M(z_3)).$$ Then if \(z\) is a root of \(p'(z)\), \(M(z)\) is a root of \(p_M'(z)\). In other words, we can transform the initial triangle \(\Delta z_1z_2z_3\) via any linear transformation and its roots will follow appropriately. ᐅ
2. For a quadratic polynomial \(p(x) = x^2 + bx + c\) with roots \(z_1\) and \(z_2\), the coefficients are given by \(b = -(z_1 + z_2)\) and \(c = z_1z_2\). ᐅ
3. Let \(f_1\) and \(f_2\) be focii of an ellipse, and let \(p\) be a point outside of the ellipse. The point \(p\) induces (exactly) two tangent lines of the ellipse which intersect \(p\); call the intersection of these lines with the ellipse \(t_1, t_2\). Then \(\angle f_1pt_1 = \angle f_2pt_2\). ᐅ

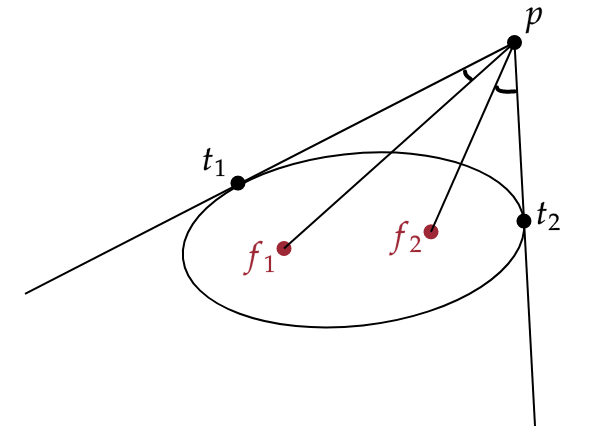
We'll break the proof down into two lemmas...

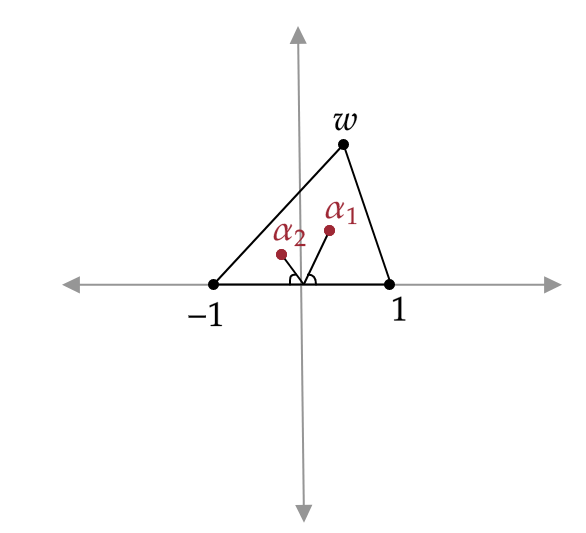
Lemma 1. Let \(T\) be the triangle in \(\mathbb{C}\) with vertices \(z_1,z_2,z_3\), which are the roots of the monic polynomial \(p(x)\). Then if the ellipse with the roots of \(p'(x)\) as the focii passes through the midpoint of one side of \(T\), it is actually tangent to that side of \(T\).

Proof. By Fact 1, we can apply some linear transformation such that the vertices of \(T\) are -1, 1, and \(w\), with \(\text{Im}(w) > 0\). We want to show that the horizontal axis is tangent to the ellipse. So we have $$ p(z) = (z-1)(z+1)(z-w) $$ and thus \begin{align*} p'(z) &= (z-1)(z+1) + (z+1)(z-w) + (z-1)(z-w)\\ &= 3(z^2 - \frac{2w}{3}z - \frac{1}{3}). \end{align*} So (by Fact 2) if \(\alpha_1\) and \(\alpha_2\) are the roots of \(p'\), they satisfy \(\alpha_1 + \alpha_2 = \frac{2w}{3}\) and \(\alpha_1\alpha_2 = -\frac{1}{3}\). In particular, thinking of \(\alpha_j = r_je^{i\theta_j}\), we see that the roots lie in the upper half-plane and that \(\theta_1 + \theta_2 = \pi\). In other words, as vectors, \(\alpha_1\) and \(\alpha_2\) are supplementary. So the angles made by the focii and the point 0 on the ellipse with the \(x\)-axis are equal. Thus, the horizontal axis is a tangent line of the ellipse. This is what we wanted to show. \(\Box\)

Lemma 2. Let \(T\) be the triangle in \(\mathbb{C}\) with vertices \(z_1,z_2,z_3\), which are the roots of the monic polynomial \(p(x)\). If the ellipse with roots of \(p'(x)\) as the focii is tangent to one side of \(T\), then it is tangent to all sides of \(T\).

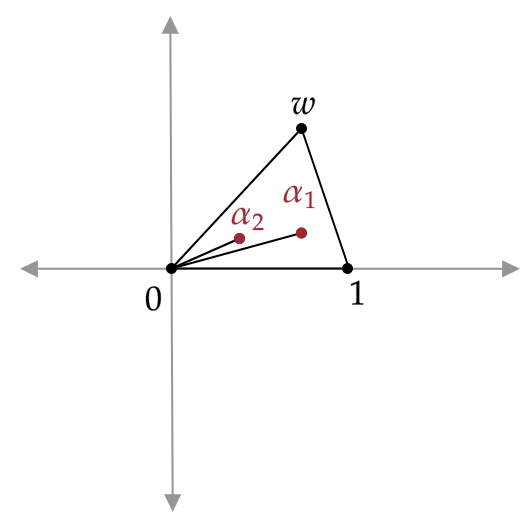
Proof. Again by Fact 1, we can let the vertices of \(T\) be 0, 1, and \(w\) for \(\text{Im}(w) > 0\). Then \begin{align*} p(z) &= z(z-1)(z-w)\\ &= z^3 - (1+w)z^2 + wz. \end{align*} Taking the derivative, we get $$ p'(z) = 3z^2 - 2(1+w)z + w.$$ By similar tactics as in Lemma 1, we see that \(\alpha_1 + \alpha_2 = 2(1+w)\) and \(\alpha_1\alpha_2 = w\). Note that both \(\alpha_1\) and \(\alpha_2\) are in the upper half-plane. Let \(\alpha_j = r_je^{i\theta_j}\) and \(w = r_we^{i\theta_w}\). Without loss, say \(\theta_1 \leq \theta_2\) So we get from the equations above that \(\theta_1 + \theta_2 = \theta_w\). In other words \(\angle10\alpha_1 = \angle w0\alpha_2\). By Fact 3 (with 0 as the point \(p\)), we get that the line \(0w\) is a tangent line to the ellipse. We can reapply this argument to the third edge (perhaps on a different linear transformation) to get the desired result. \(\Box\)

We now have the material to prove the theorem.

Proof of Marden's Theorem. Let \(E\) be the ellipse of a polynomial \(p\) tangent to one side of the induced triangle \(T\) as constructed in Lemma 1. By Lemma 2, \(E\) is actually tangent to the other two sides. The points of tangency with the other two sides must be at the midpoints, because if not, we could repeat the construction with the other two sides, giving us three non-identical ellipses with the same focii tangent to the same three lines. But this can't happen. \(\Box\)