Complex Analysis

Peter Zenz - Fall 2022

Lecture 1 — Introduction, Complex Numbers, and Polar Coordinates
Lecture 2 — Polar Coordinates and Complex Exponentials
Lecture 3 — Complex Exponentials, Logarithms, and Power Functions

Feel free to copy, reuse, and distribute any part of these notes. Please email ian [at] beanway [dot] me with any errors!

Lecture 1 - Introduction, Complex Numbers, and Polar Coordinates

Introduction and Overview

Complex analysis studies complex numbers! We can define all complex numbers like $$ \mathbb{C} := \{x + yi\:|\: x,\,y\in\mathbb{R}\} \;\;\;\;\text{when}\;\;\;\; i^2 = -1. $$ When we consider $\mathbb{C}$, it's kind of like $\mathbb{R}$ in the sense that it's a field. It's also a lot like $\mathbb{R}^2$ in the sense that there is a one-to-one correspondence between the complex plane and the $\mathbb{R}^2$ plane. But it's also different in interesting ways. For example, if a function over the complex numbers is differentiable, then you can differentiate it infinitely many times.

We know from calculus that $$ \sum_{n=1}^{\infty}\frac{1}{n^x} $$ is convergent for $x>1$. But what if we replace $x$ with a complex number $s$? This is a famous function, the Riemann Zeta Function: $$ \zeta(s) = \sum_{n=1}^{\infty}\frac{1}{n^s} $$ where $s \in \mathbb{C}$ and $Re(s) > 1$.

The zeta function is defined for Re(z) > 1.

If we consider $\zeta(-1)$, we get something like $$ \zeta(-1) = 1 + 2 + 3 + \cdots = -1/12. $$ By the end of this course, we'll see how this can make sense. The zeta function ties into analytic number theory in finding prime numbers.

Complex Definitions

We'll now define some basic operations. If $z = x + yi$, then $x = Re(z)$ and $y = Im(z)$.

Addition: $(a + bi) + (c + di) = (a + c) + (b + d)i$
Multiplication: $ (a + bi)(c + di) = ac - bd + i(da + bc) $

These both satisfy associativity, commutativity, and distributivity.

Modulus/Absolute Value: $ |z| = |x + yi| := \sqrt{x^2 + y^2} $

This satisfies the triangle inequality: $ |w \pm z| \leq |w| + |z| $.

Division: For $z = x + yi \neq 0$, we want an $a + bi$ such that $$ (x + yi)(a + bi) = 1. $$ $a + bi = \frac{1}{x + yi} \cdot \frac{x - yi}{x - yi} = \frac{x-yi}{x^2 + y^2}$, so $a=\frac{x}{x^2+y^2}$ and $b=\frac{-y}{x^2+y^2}$.

Complex Conjugation: $ \overline{x + yi} = x - yi $
- $\bar{\bar{z}} = z$
- $\overline{z+w} = \overline{z} + \overline{w}$
- $\overline{zw} = \overline{z} \cdot \overline{w} $
- $|z| = |\overline{z}|$
- $ |z|^2 = z\overline{z} $
- $ Re(z) = \frac{z + \overline{z}}{z} \;\; ; \;\;\ Im(z) = \frac{z - \overline{z}}{z} $
- $ |zw| = |z||w| $

Polar Coordinates

Here, we're considering use of different coordinate systems. We can see that $$ x = r\cdot \cos{\theta} $$ $$ y = r\cdot \sin{\theta} $$ and so $$ z = x + yi = r(\cos{\theta} + i\sin{\theta}) $$ with $r = \sqrt{x^2 + y^2} = |z|$.

We call $\theta$ the argument of $z$. Because this $\theta$ is brought from a multivalued function, we want to denote a principal value of $arg(z)$, denoted by $Arg(z)$, as $\theta$ restricted between $-\pi < \theta \leq \pi $.

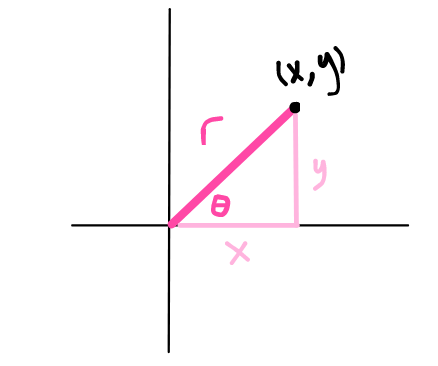
Lecture 2 — Polar Coordinates and Complex Exponentials

Complex Multiplication Geometrically

Firstly, we can see that $Arg(i) = \frac{\pi}{2} $

by the geometry of polar coordinates.

For complex numbers $z$ and $w$, we can write $$ \begin{align} z &= r(\cos\theta + i\sin\theta) \\ w&= s(\cos\phi + i\sin\phi). \end{align} $$ So, $$ \begin{align} zw &= rs((\cos\theta\cos\phi - \sin\theta\sin\phi) + i(\sin\theta\cos\phi + \cos\theta\sin\phi)) \\ &= rs(\cos(\theta + \phi) + i\sin(\theta+\phi)). \end{align} $$ Meaning that multiplying two complex numbers becomes multiplying their lengths and adding their angles.

Facts from Real Analysis

Let $a_n \in \mathbb{C} $. We say that $ \displaystyle\sum_{n=0}^{\infty} a_n $ converges iff partial sums $ S_N = \displaystyle\sum_{n=0}^{N} a_n $ converge. We define convergence as there existing an $ S \in \mathbb{C} $ so that $ \displaystyle\lim_{N \to\infty} |S_N - S| = 0. $

We'll need the following facts:

For every $ r \in \mathbb{R}, \,\, \displaystyle\sum_{n=0}^{\infty}\frac{r^n}{n!} $ converges.
If $ a_n \in \mathbb{C} $ and $ \displaystyle\sum_{n=0}^{\infty}|a_n| $ converges, then $ \displaystyle\sum_{n=0}^{\infty} a_n $ converges.
If $ \displaystyle\sum_{n=0}^{\infty} a_n $ and $ \displaystyle\sum_{n=0}^{\infty} b_n $ converge absolutely, then $ \displaystyle\sum_{n=0}^{\infty}\displaystyle\sum_{k=0}^{n}a_nb_{n-k}$ converges to $ \displaystyle\sum_{n=0}^{\infty}a_n\displaystyle\sum_{m=0}^{\infty}b_m $.

Complex Exponentials

Here, we want to generalize the exponential function $ e^x $ to work on complex numbers. What does raising a number to a complex number even mean? Well, we can take the summation definition of $e^x$: $$ e^z := 1 + z + \frac{z^2}{2!} + \frac{z^3}{3!} + \cdots = \sum_{n=0}^{\infty}\frac{z^n}{n!}. $$ We said this converges for all $z \in \mathbb{C}$, so it's well-defined on the complex numbers. Now, we can check its properties with some analysis: $$\begin{align} e^xe^y &= \sum_{k=0}^{\infty}\frac{x^k}{k!}\sum_{l=0}^{\infty}\frac{y^l}{l!} \\ &= \sum_{k=0}^\infty \sum_{n=k}^\infty \frac{x^ky^{n-k}}{k!(n-k)!} \;\;\;\;\;\;\text{ where we let $l = n - k$} \\ &= \sum_{n=0}^\infty \frac{1}{n!}(\sum_{k=0}{n}\begin{pmatrix} n \\ k \end{pmatrix} x^ky^{n-k}) \\ &= \sum_{n=0}^{\infty}\frac{1}{n!}(x+y)^n \\ &= e^{x + y}. \end{align}$$

So, we've just shown that $ e^xe^y = e^{x+y} $. This is nice because it means that $$ e^{x+iy} = e^x\cdot e^{iy}. $$ Well, $ e^{iy} = \displaystyle\sum_{n=0}^\infty \frac{(iy)^n}{n!} $. We know that $ i^2 = -1 $, $i^3 = -i$, and $i^4 = 1$, so $$ e^{x+iy} = e^x\cdot e^{iy} = \sum_{k=0}^{\infty}{(-1)^k \frac{y^{2k}}{(2k)!}} + i\sum_{k=0}^\infty { (-1)^k \frac{y^{2k}+1}{(2k+1)!} }. $$ But notice that the first part is the summation definition of $\cos y$ and the second part is the summation definition of $ i\sin y $. So what we have is

$$ e^{iy} = \cos y + i\sin y. $$

So we can write any $ z \in \mathbb{C}$ as $z = re^{i\theta} = r(\cos\theta + i \sin\theta)$.

So, $ e^{i\pi} = \cos\pi + i\sin\pi = -1 $.

Lecture 3 — Complex Exponentials, Logarithms, and Power Functions

Recall we can write $ z = re^{i\theta} $. We defined exponentiating complex numbers, but how does this exponentiation function act?

Properties:

$ |e^{i\theta}| = 1 = \sqrt{\cos^2\theta + \sin^2\theta} $
$ e^{\overline{i\theta}} = e^{-i\theta} $
$ \frac{1}{e^{i\theta}} = e^{-i\theta} $

What does it look like? Well, on the complex plane, it maps horizontal lines to rays and vertical lines to circles.

Proving Trig Identities From Exponentials

Recall that $ e^{i(\theta + \phi)} = e^{i\theta} \cdot e^{i\phi} $. This implies that $$ \begin{align} \cos(\theta + \phi) + i\sin(\theta + \phi) &= (\cos\theta + i\sin\theta)(\cos\phi + i\sin\phi) \\ &= \cos\theta\cos\phi - \sin\theta\sin\phi + i(\sin\theta\cos\phi + \cos\theta\sin\phi) \end{align}.$$

Complex Logarithms

We want to invert $ e^z $. There's a problem: $ e^z $ is not injective. (Compare this relationship with $\sin x$ and $\arcsin x$ restricted to $[-1, 1]$.) Here's how we can do it:

For $z \neq 0 \in \mathbb{C}$, we define $$\begin{align} \log z &= \log |z| + arg(z) \\ &= \log |z| + iArg(z) + 2\pi ik. \end{align}$$

Values of $\log z$ are complex numbers such that $e^w = z$ $$\begin{align} e^2 = e^{\log z} &= e^{\log |z|}e^{iArg(z)}e^{2\pi ik}\\ &= |z| \cdot e^{iArg(z)} \cdot 1 = z. \end{align}$$

On the other hand, suppose $w = u + iv$ such that $e^2 = z = re^{i\theta}$. Then, $$\begin{align} r = |z| = e^u \Rightarrow u = \log |z|\;\; \text{ and }\;\; v = arg (z). \end{align}$$

The principal value of $ \log z $ is defined by $ \text{Log }(z) = \log |z| + iArg(z). $

Note: $\log z$ is a multivalued function, but $\text{Log } z$ is a single-valued function with values in the horizontal strip $-\pi < Im(z) \leq \pi$.

Compute $\text{Log } i$: $$\begin{align} \text{Log } i &= \log |i| + iArg(i) \\ &= log(1) + i\frac{\pi}{2} &= \frac{i\pi}{2} \end{align}$$

Power Functions

For $z,\,\alpha \in \mathbb{C}$ where $z \neq 0$, we can define a general power function as $$ z^\alpha := e^{\alpha\log z}. $$ So, $$ e^{\alpha(\log |z| + iArg(z) + 2\pi ik)}. $$

So we can now use exponents with complex numbers more generally. But we should be careful! Because things don't behave exactly like the reals here. The power rule of distribution doesn't hold, i.e. $$ z^\alpha z^\beta \neq z^{\alpha + \beta}. $$

Lecture 4 —

Complex Roots

We want some $ w \in \mathbb{C} $ such that $ w^2 = z $. We'll write $z = re^{i\theta}$ and $ w = se^{i\phi} $. Then, $$ w^2 = s^2e^{i2\phi} = re^{i\theta}. $$ This means that $$ s^2 = r \;\;\;\; \text{and} \;\;\;\; 2\phi = \theta. $$ So we conclude that $ w = \sqrt{r}e^{i\theta / 2} $. But there's another solution: $ w = \sqrt{r}e^{i(\frac{\theta}{2} + \pi)} $. Note that there are two solutions.

In general, an $ n^{\text{th}} $ root has $n$ solutions in $\mathbb{C}$.

General $n^{\text{th}}$ Root
We want $w\in\mathbb{C}$ where $w^n = z$. Well we have $$\begin{align} \Leftrightarrow& s^ne^{in\phi} = re^{i\theta}\\ \Leftrightarrow& s^n = r \;\;\;\;\text{and}\;\;\;\;n\phi = \theta + 2\pi k\end{align}$$ So, $s = \sqrt[n]{r}$ and $ \phi = \frac{\theta}{n} + \frac{2\pi k}{n} $ with $ k = 0,\dots,n-1 $.

Compute the square root of $ z = -1 - i $.
Well, $ -1 - i = \sqrt{2}e^{i\frac{5\pi}{4}} $. We get $w_1 = \sqrt[4]{2}e^{i\frac{5\pi}{8}}$ and $ w_2 = \sqrt[4]{2}e^{i\frac{13\pi}{8}} $.